Questõessobre Geometria Analítica

InícioTodas as questões
1
1
Foram encontradas 214 questões
af79b5fa-ff
URCA 2016 - Matemática - Pontos e Retas, Geometria Analítica

A região do plano delimitada pelas retas x = 0, y = 0, a reta que passa por (−3,4) e (0,2) e a reta 5x + 6y − 30 = 0 possui área igual a:

A
12u . a.
B
18u . a.
C
24u . a.
D
32u . a.
E
35u . a.
4d064ee8-fd
ESPM 2018 - Matemática - Pontos e Retas, Geometria Analítica

Uma praça tem a forma de um quadrado de 200 m de lado. Partindo juntas de um mesmo canto P, duas amigas percorrem o perímetro da praça caminhando em sentidos opostos, com velocidades constantes. O primeiro encontro delas se dá em um ponto A e o segundo, em um ponto B. Se a medida do segmento PA é 250 m, então, o segmento PB mede:

A
50 m
B
100 m
C
150 m
D
200 m
E
250 m
4d105c8e-fd
ESPM 2018 - Matemática - Pontos e Retas, Geometria Analítica

A figura abaixo representa uma parte de um bairro, onde os segmentos são as ruas e os pontos são as esquinas. Como só podemos caminhar pelas ruas, a distância entre os pontos A e B é de 6 quarteirões.


O número de esquinas assinaladas no mapa, que são equidistantes de A e B, é igual a:

A
5
B
6
C
9
D
8
E
7
cf363e27-fa
UFRGS 2019 - Matemática - Pontos e Retas, Geometria Analítica

Um aplicativo de transporte disponibiliza em sua plataforma a visualização de um mapa com ruas horizontais e verticais que permitem realizar deslocamentos partindo do ponto A e chegando ao ponto B, conforme representado na figura abaixo.




O número de menores caminhos possíveis que partem de A e chegam a B, passando por C, é

A
28.
B
35.
C
100.
D
300.
E
792.
cf17977c-fa
UFRGS 2019 - Matemática - Pontos e Retas, Geometria Analítica, Polígonos, Geometria Plana

A figura a seguir é formada por quadrados de lados , e assim sucessivamente.

A construção é tal que os pontos P1, P2, P3, ... , B são colineares, e as bases dos quadrados têm medidas e assim por diante. O ponto A é vértice do quadrado de lado como representado na figura abaixo.



A medida do segmento é

A
1.
B
√2.
C
√3.
D
2.
E
√5.
bb71a1c7-f7
UEG 2016 - Matemática - Pontos e Retas, Geometria Analítica, Geometria Plana, Triângulos

Na figura a seguir, os pontos A, B, C formam um triângulo equilátero de lado x, os pontos A, C, D, E um quadrado e o segmento BF é o dobro do tamanho de CD.




Considerando-se os dados apresentados, verifica-se que a distância do ponto F ao ponto E é

A

B


C
x2 + √3x
D

E
x2(8 + √3)
bb6eb097-f7
UEG 2016 - Matemática - Pontos e Retas, Geometria Analítica

Na figura a seguir, as retas r, s , t, u são paralelas e seus coeficientes lineares estão em uma progressão aritmética de razão - 2.



Sabendo-se que a equação da reta p é y = x + 3 e da reta u é y = 3x - 5 , o ponto de intersecção da reta p com a reta s é

A

B

C

D

E

216dc473-f7
UEG 2015 - Matemática - Circunferências, Geometria Analítica

Uma circunferência de centro (-1,0) e raio 3 é interceptada por uma reta. Sabendo-se que os pontos e (-√2, √2 + 2) pertencem à reta, a soma das coordenadas do eixo-x dos pontos de intersecção é

A
-1
B
0
C
1
D
√2
4ba77143-8f
UNICAMP 2021 - Matemática - Pontos e Retas, Geometria Analítica

No plano cartesiano, considere a reta de equação x + 2y = 4, sendo A, B os pontos de interseção dessa reta com os eixos coordenados. A equação da reta mediatriz do segmento de reta AB é dada por

A
2x - y = 3.
B
2x - y = 5.
C
2x + y = 3.
D
2x + y = 5.
0c9634ac-88
CEDERJ 2020 - Matemática - Pontos e Retas, Geometria Analítica, Funções, Função de 1º Grau

As retas definidas pela equações 2x + ky - 6 = 0 e -4x + (k - 1)y + 1 = 0 são paralelas.

O número real k é igual a:

A
1/3
B
1/4
C
1/5
D
1/6
c2e7b945-7f
IMT - SP 2020 - Matemática - Pontos e Retas, Geometria Analítica, Geometria Plana, Ângulos - Lei Angular de Thales

Uma lâmina deve ser confeccionada com a forma apresentada na figura, em que é paralelo a igual a 80º e igual a 35º .



A medida do ângulo , é

A
120°
B
90°
C
115°
D
65°
E
45°
c2da64b3-7f
IMT - SP 2020 - Matemática - Pontos e Retas, Geometria Analítica

Na figura, a reta s é paralela à reta r, e a reta t paralela à reta u. Sabe-se que a distância da reta r à reta s é igual a distância entre as retas t e u, que é 2 cm.


A área do paralelogramo delimitado por essas retas mede 8 cm2 . Nessas condições, o valor do sen

A

B
1/2
C
1/4
D

E

eb224d35-7f
IMT - SP 2020 - Matemática - Circunferências, Álgebra, Pontos e Retas, Geometria Analítica, Produtos Notáveis e Fatoração

Considere, no plano cartesiano, a circunferência C de equação (x-1)² + (y-1)² = 1 e o ponto A de coordenadas (1,3) . Uma reta t, com coeficiente angular negativo, passa por A e é tangente a C em um ponto B. É correto afirmar que as distâncias de A a B e do ponto de intersecção da reta t com o eixo das abcissas até a origem do sistema de coordenadas são, respectivamente,

A

B

C
2 e 5/2
D
1 e 4
E

de87db8a-7b
USP 2021 - Matemática - Circunferências, Geometria Analítica



A região hachurada do plano cartesiano xOy contida no círculo de centro na origem O e raio 1, mostrada na figura, pode ser descrita por 


Note e adote:

círculo de centro O e raio 1 é o conjunto de todos os pontos do plano que estão a uma distância de O menor do que ou igual a 1.

A
{(x, y); x2 + y2 ≤ 1 e y — x ≤ 1}.
B
{(x, y); x2 + y2 ≥ 1 e y + x ≥ 1}.
C
{( x ,y ) ; x2 + y 2 ≤ 1 e y - x ≥ 1}
D
{(x, y); x 2 + y 2 ≤ 1 e y + x ≥ 1}.
E
{(x, y); x 2 + y 2 ≥ 1 e y + x ≤ 1}.
61aa93a0-76
UNIVESP 2017 - Matemática - Pontos e Retas, Geometria Analítica

O valor de x para que os pontos (x,2), (x,4) e (3x,4), num plano cartesiano (x, y), formem um triângulo de área igual a 10 é

A
1
B
3
C
5
D
7
E
9
618c1c8b-76
UNIVESP 2017 - Matemática - Pontos e Retas, Geometria Analítica

No plano cartesiano (x,y), considere uma reta r que passa pelos pontos (1, 2) e (3, –2), e uma retas, que passa pelo ponto (4, 4) e (5, 2). É correto afirmar que as retas r e s são

Dado:
∆y/∆x

A
perpendiculares.
B
concorrentes oblíquas.
C
paralelas distintas.
D
coincidentes.
E
reversas.
dc1551fc-6e
UPE 2021 - Matemática - Pontos e Retas, Geometria Analítica

Uma estrada retilínea é representada no plano cartesiano ortogonal por uma reta que contém os pontos (-4, 9) e (12, 1), coordenadas que representam duas placas de sinalização na estrada. Qual dos pontos a seguir pode representar uma placa de sinalização pertencente a essa estrada?

A
(7, 4)
B
(- 10, 12)
C
(8, 5)
D
(-1, 15)
E
(- 2, 7)
dc0266f1-6e
UPE 2021 - Matemática - Pontos e Retas, Geometria Analítica

Flávia, aluna do 3º ano do Ensino Médio, em uma aula de matemática, traçou os eixos x e y do sistema cartesiano ortogonal na malha abaixo e, em seguida, marcou os pontos A (-3, 1), B (0, 4), C (5, 4) e D (-2, -3). Se os quadradinhos da malha têm lado unitário, qual é a medida da área do quadrilátero cujos vértices são os pontos A, B, C e D do plano cartesiano criado por Flávia?



A
14 √2
B
22
C
18 √2
D
24
E
25
9ef994ee-5f
ENEM 2020 - Matemática - Geometria Analítica, Cônicas

No período de fim de ano, o síndico de um condomínio resolveu colocar, em um poste, uma iluminação natalina em formato de cone, lembrando uma árvore de Natal, conforme as figuras 1 e 2.


A árvore deverá ser feita colocando-se mangueiras de iluminação, consideradas segmentos de reta de mesmo comprimento, a partir de um ponto situado a 3 m de altura no poste até um ponto de uma circunferência de fixação, no chão, de tal forma que esta fique dividida em 20 arcos iguais. O poste está fixado no ponto C (centro da circunferência) perpendicularmente ao plano do chão.

Para economizar, ele utilizará mangueiras de iluminação aproveitadas de anos anteriores, que juntas totalizaram pouco mais de 100 m de comprimento, dos quais ele decide usar exatamente 100 m e deixar o restante como reserva.

Para que ele atinja seu objetivo, o raio, em metro, da circunferência deverá ser de

A
4,00.
B
4,87.
C
5,00.
D
5,83.
E
6,26.
11ce52e9-03
UniREDENTOR 2020 - Matemática - Pontos e Retas, Circunferências e Círculos, Geometria Analítica, Geometria Plana



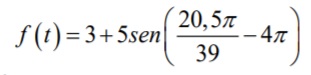
A equação representa uma circunferência no plano cartesiano, dessa forma, pode-se dizer que a soma das coordenadas do centro da circunferência é equivalente a:


A
-5
B
-6
C
- 7 1
D
-8
E
-9