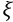Um grão de milho de pipoca, visto a olho nu,
apresenta duas regiões distintas,
representadas por A e B na figura. Em A,
ocorre o tecido acumulador de amido, usado,
pela planta, para nutrir o embrião. Em B, os
tecidos vegetais possuem maior teor de água.
Ao ser aquecida, parte da água transforma‐se em vapor,
aumentando a pressão interna do grão. Quando a temperatura
atinge 177°C, a pressão se torna suficiente para romper o grão,
que vira uma pipoca.
Um estudo feito por um grupo de pesquisadores determinou
que o interior do grão tem 4,5 mg de água da qual, no momento
imediatamente anterior ao seu rompimento, apenas 9% está
na fase vapor, atuando como um gás ideal e ocupando 0,1 mL.
Dessa forma, foi possível calcular a pressão Pfinal no momento
imediatamente anterior ao rompimento do grão.
A associação correta entre região do milho e Pfinal é dada por:
Note e adote:
Constante universal dos gases: R = 0,082 L.atm/(K.mol);
K = °C + 273;
Massas molares (g/mol): H = 1; O = 16.


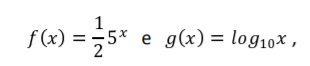




























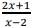 e a
função ݃
e a
função ݃
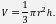
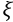 cuja parte imaginária é positiva. A parte real de
cuja parte imaginária é positiva. A parte real de