Se f e g são funções reais definidas por 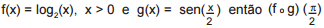 é igual a
é igual a
Se f e g são funções reais definidas por 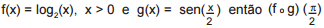 é igual a
é igual a
Se f e g são funções reais definidas por 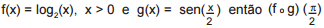 é igual a
é igual a
Observando-se o céu após uma chuva, avista-se parte de um arco-íris atrás de uma construção. A parte visível poderia ser identificada como a representação gráfica da função f dada por f (x) = log x, abaixo.

A soma dos valores a, b e c, indicados na fi gura, é





Sendo f : R2 – {(0, 0)} → R a função definida por f(x, y) = ln(x2 + 4y2), é correto afirmar:
Todas as curvas de nível de f são elipses.
Sendo f : R2 – {(0, 0)} → R a função definida por f(x, y) = ln(x2 + 4y2), é correto afirmar:
O gráfico de f é simétrico em relação à origem.
Considerando-se f : R → R a função definida por f(x) = 1/2 ln(x2 + 1), é correto afirmar:
f possui um ponto de máximo local em x = 0.
Considerando-se f : R → R a função definida por f(x) = 1/2 ln(x2 + 1), é correto afirmar:
f é crescente no intervalo ] – ∞, 0 [.
 tal que
tal que 






 (x2 - 6x + 9 ) =
(x2 - 6x + 9 ) =  (x - 2 ) onde ∪ = { x ∪ ℜ/ x > 2 e x ≠ 3 } é o seu conjunto universo.
(x - 2 ) onde ∪ = { x ∪ ℜ/ x > 2 e x ≠ 3 } é o seu conjunto universo.

