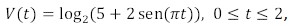Sendo f : R2 – {(0, 0)} → R a função definida por f(x, y) = ln(x2 + 4y2), é correto afirmar:
Todas as curvas de nível de f são elipses.
Sendo f : R2 – {(0, 0)} → R a função definida por f(x, y) = ln(x2 + 4y2), é correto afirmar:
Todas as curvas de nível de f são elipses.

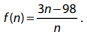 Para alguns valores inteiros de
Para alguns valores inteiros de  mas, para
mas, para
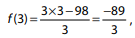 que não é um número inteiro.
O número de valores inteiros de
que não é um número inteiro.
O número de valores inteiros de
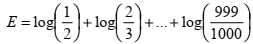 é .
é .

 julgue o item que se segue.
julgue o item que se segue.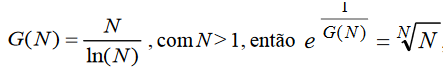 , em que e é a base do logaritmo natural.
, em que e é a base do logaritmo natural.