Em uma comunidade, o número aproximado de pessoas que toma conhecimento de determinado
fato, t meses após ele ter ocorrido, pode ser estimado através do modelo matemático definido
pela função 
A partir dessa expressão, considerando-se log 2 = 0,30 e log 3 = 0,48, para que 375 pessoas
tomem conhecimento de um fato, após a sua ocorrência, estima-se que o número de dias
necessários é igual a

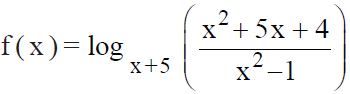 está definida, é
está definida, é










