Com base nessas informações, julgue o próximo item.
Se 0 < A < 5, então a população P(t) é crescente.
Com base nessas informações, julgue o próximo item.
Se 0 < A < 5, então a população P(t) é crescente.
Estimar a quantidade de indivíduos da população mundial
futura é um desafio complexo. O modelo logístico baseia-se na
hipótese de que, com o passar dos anos, a população mundial deve
estabilizar-se em certo valor A ≠ 0, denominado população limite.
Segundo esse modelo, a população, P(t), de seres humanos no
planeta, em bilhões de habitantes, a partir de 1987, obedece
à equação  em que t é a quantidade de
anos a partir de 1987, que é o instante inicial e corresponde a t = 0;
5 bilhões é a população no ano de 1987; A é a população limite; e
r é uma constante positiva.
em que t é a quantidade de
anos a partir de 1987, que é o instante inicial e corresponde a t = 0;
5 bilhões é a população no ano de 1987; A é a população limite; e
r é uma constante positiva.
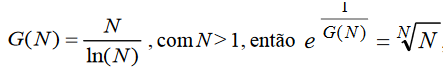 , em que e é a base do logaritmo natural.
, em que e é a base do logaritmo natural.





 é o número de átomos instáveis do material referido acima que ainda não se desintegraram, então, em
é o número de átomos instáveis do material referido acima que ainda não se desintegraram, então, em  restarão
restarão  átomos instáveis desse material que ainda não se desintegraram
átomos instáveis desse material que ainda não se desintegraram em meio rico em triptofano, é 1 sempre menor que a população
em meio rico em triptofano, é 1 sempre menor que a população  em meio sem triptofano.
em meio sem triptofano.

 em meio que não contém triptofano, chegue a 27 mil indivíduos.
em meio que não contém triptofano, chegue a 27 mil indivíduos.