Questões sobre Equações Exponenciais

3b22b085-9b

FGV 2017 - Matemática - Funções, Equações Exponenciais

Uma epidemia em ratos propaga-se da seguinte forma: cada rato infectado contamina três outros ratos em uma semana. Mantendo-se essa taxa de contaminação, após a contaminação do primeiro rato,

A

em duas semanas tem-se exatamente 6 ratos contaminados.

B

em três semanas mais de 100 ratos estarão contaminados.

C

em quatro semanas mais de 1.000 ratos estarão contaminados.

D

em cinco semanas mais de 2.000 ratos estarão contaminados.

E

em seis semanas mais de 4.000 ratos estarão contaminados.

821048f1-74

CEDERJ 2018 - Matemática - Função Logarítmica, Funções, Equações Exponenciais, Função de 2º Grau

Considere a função de variável real x definida por

Determinando a quantidade de números reais distintos que fazem parte do domínio de f e que são soluções da equação f(x) = 0, encontramos

A

3

B

4

C

5

D

6

3336da17-58

UNESP 2018 - Matemática - Análise de Tabelas e Gráficos, Funções, Equações Exponenciais

Observe, no plano cartesiano de eixos ortogonais, o gráfico de duas funções exponenciais de

A intersecção desses gráficos ocorrerá em

A

infinitos pontos, localizados no 2° quadrante.

B

um único ponto, localizado no 2° quadrante.

C

um único ponto, localizado no 3° quadrante.

D

um único ponto, localizado no 1° quadrante.

E

um único ponto, localizado no 4° quadrante.

1aaaaca2-4b

ENEM 2014 - Matemática - Equações Exponenciais

Pesquisas indicam que o número de bactérias X é duplicado a cada quarto de hora. Um aluno resolveu fazer uma observação para verificar a veracidade dessa afirmação. Ele usou uma população inicial de 105 bactérias X e encerrou a observação ao final de uma hora.

Suponha que a observação do aluno tenha confirmado que o número de bactérias X se duplica a cada quarto de hora.

Após uma hora do início do período de observação desse aluno, o número de bactérias X foi de

A

2-2 . 105

B

2-1 . 105

C

22 . 105

D

23 . 105

E

24 . 105

10068b31-4e

ENEM 2013 - Matemática - Funções, Equações Exponenciais

Em um experimento, uma cultura de bactérias tem sua população reduzida pela metade a cada hora, devido à ação de um agente bactericida.

Neste experimento, o número de bactérias em função do tempo pode ser modelado por uma função do tipo

A

afim.

B

seno.

C

cosseno.

D

logarítmica crescente.

E

exponencial.

1e7913e7-4c

ENEM 2011 - Matemática - Funções, Equações Exponenciais

A torre de Hanói é um jogo que tem o objetivo de mover todos os discos de uma haste para outra, utilizando o menor número possível de movimento, respeitando-se as regras.

As regras são:
1- um disco maior não pode ser colocado sobre um disco menor;
2- pode-se mover um único disco por vez;
3- um disco deve estar sempre em uma das três hastes ou em movimento.
Disponível em: http://www.realidadevirtual.com.br. Acesso em: 28 abr. 2010 (adaptado).
Disponível em: http://www.imeusp.br. Acesso em: 28 abr. 2010 (adaptado).

Usando a torre de Hanói e baseando-se nas regras do jogo, podemos montar uma tabela entre o número de peças (X) e o número mínimo de movimentos (Y):

A relação entre (X) e (Y) é

A

Y = 2X - 1

B

Y = 2X-1

C

Y = 2X

D

Y = 2X - 1

E

Y = 2X - 4

f81943cb-4a

ENEM 2015 - Matemática - Funções, Equações Exponenciais

O sindicato de trabalhadores de uma empresa sugere que o piso salarial da classe seja de R$ 1 800,00, propondo um aumento percentual fixo por cada ano dedicado ao trabalho. A expressão que corresponde à proposta salarial (s), em função do tempo de serviço (t), em anos, é s(t) = 1 800 (1,03)t .

De acordo com a proposta do sindicato, o salário de um profissional de empresa com 2 anos de tempo de serviço será, em reais,

A

7 416,00.

B

3 819,24.

C

3 709,62.

D

3 708,00.

E

1 909,62.

c6dbc36d-49

UNB 2010 - Matemática - Função Logarítmica, Aritmética e Problemas, Números Primos e Divisibilidade, Funções, Equações Exponenciais

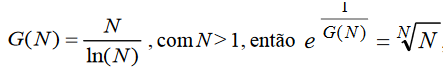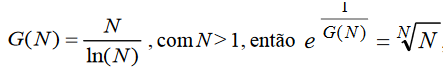Se , em que e é a base do logaritmo natural.

A respeito do assunto abordado no texto acima, assinale a opção
correta e julgue o item.

C

Certo

E

Errado

1462829f-49

UNB 2010 - Matemática - Função Logarítmica, Seno, Cosseno e Tangente, Trigonometria, Funções, Funções Trigonométricas e Funções Trigonométricas Inversas, Logaritmos, Equações Exponenciais

Para se trabalhar com a “escala inimaginável de tempo” mencionada no último parágrafo do texto, poderia ser feita uma transformação que associa cada número da escala a um bem menor, de modo que a quantidade de zeros fosse drasticamente reduzida. Por exemplo, o número 10¹⁰⁰(1 seguido de 100 zeros) pode ser associado ao número 100. A função matemática que tem essa propriedade é a

Considerando o texto acima, julgue o item e assinale a
opção correta.

A

exponencial.

B

logarítmica.

C

tangente.

D

seno.

3546d1eb-3b

UFPR 2016 - Matemática - Funções, Equações Exponenciais

Suponha que a quantidade Q de um determinado medicamente no organismo t horas após sua administração possa ser calculada pela fómula:
Q = 15 . (1/10)2t

sendo Q medindo em miligramas. A expressão que fornece o tempo t em função da quantidade de medicamento Q é:

A

t = log√15/Q

B

t = log15/2logQ

C

t = 10√log(Q/15)

D

t =1/2 log Q/15

E

t = log Q2/225

61066eb2-30

PUC - RS 2016 - Matemática - Funções, Equações Exponenciais

Observe, na figura abaixo, uma parte da rampa em uma pista de skate. Sua forma é semelhante à representação gráfica de uma função em que y = f(x) é dada por

A

y = ax + b, a ≠ 0

B

y = | ax |, a ≠ 0

C

y = √ax , a ≠ 0

D

y = loga (x), a > 1

E

y = ax , a > 1

6e4291c5-1d

UNICAMP 2016 - Matemática - Álgebra, Problemas, Funções, Equações Exponenciais

Considere as funções f (x) = 3x e g(x) = x3 , definidas para todo número real x. O número de soluções da equação f (g(x)) = g(f(x)) é igual a

A

1.

B

2.

C

3.

D

4.

8517daaa-c0

PUC - PR 2016 - Matemática - Funções, Equações Exponenciais

As leis governamentais dos Estados Unidos exigem que, antes que o querosene possa ser usado como combustível de jatos, deve haver a remoção dos poluentes do querosene com uso de argila. A argila fica no interior de um tubo e cada metro do tubo remove 20% dos poluentes que entram nele. Seja P₀ a quantidade inicial de poluentes e P = f(n) a quantidade de poluentes que ainda permanecem após n metros da tubulação, a função P = f(n) que melhor representa a quantidade de poluentes retidos no tubo é

A

P = P₀(1,8) n²

B

P = P₀(0,8)n

C

P = P₀(0,2)n

D

P = P₀(1,2)n

E

P = P₀(0,8)n

434d88f1-be

ENEM 2016 - Matemática - Funções, Equações Exponenciais, Inequação Logarítmica

Admita que um tipo de eucalipto tenha expectativa de crescimento exponencial, nos primeiros anos após seu plantio, modelado pela função y(t) = at -1, na qual y representa a altura da planta em metro, t é considerado em ano, e a é uma constante maior que 1 . O gráfico representa a função y.

Admita ainda que y(0) fornece a altura da muda quando plantada, e deseja-se cortar os eucaliptos quando as mudas crescerem 7,5 m após o plantio.
O tempo entre a plantação e o corte, em ano, é igual a

A

3.

B

4.

C

6 .

D

log2 7.

E

log2 15.

42afa14e-be

ENEM 2016 - Matemática - Funções, Equações Exponenciais

O governo de uma cidade está preocupado com a possível epidemia de uma doença infectocontagiosa causada por bactéria. Para decidir que medidas tomar, deve calcular a velocidade de reprodução da bactéria. Em experiências laboratoriais de uma cultura bacteriana, inicialmente com 40 mil unidades, obteve-se a fórmula para a população:
p(t) = 40 • 23t em que t é o tempo, em hora, e p(t) é a população, em milhares de bactérias.
Em relação à quantidade inicial de bactérias, após 20 min, a população será

A

reduzida a um terço.

B

reduzida à metade.

C

reduzida a dois terços.

D

duplicada.

E

triplicada.

84abb9a5-b6

PUC - RJ 2016 - Matemática - Funções, Equações Exponenciais

Assinale o gráfico que melhor representa a curva de equação y = 1/x2 .

A

B

C

D

E

33bb55a9-8a

UECE 2015 - Matemática - Funções, Equações Exponenciais

Seja R+ o conjunto dos números reais positivos e f : R → R+ a função definida por f(x) = 2x . Esta função é invertível. Se f-1 : R+ → R é sua inversa, então, o valor de f-1 (16) – f-1 (2) – f-1 (1) é

A

3.

B

8.

C

7.

D

5.

cfb26dbc-29

UNESP 2016 - Matemática - Funções, Equações Exponenciais

A figura descreve o gráfico de uma função exponencial do tipo y = ax , de |R em |R.

Nessa função, o valor de y para x = –0,5 é igual a

A

log5

B

log₅2

C

√5

D

log₂5

E

2,5

6c20df12-24

PUC-GO 2015 - Matemática - Funções, Equações Exponenciais

O Texto 6 apresenta o fenômeno de envelhecimento precoce do personagem narrador, provocado pela progéria. Funções são importantes na descrição de fenômenos científicos dessa natureza. Por exemplo, na descrição de alguns crescimentos populacionais sem inibição, podemos usar a função y = f(t) = kect, em que t representa o tempo, e f(t) a quantidade de elementos da população. Sabe-se que, num determinado momento, uma população é constituída de 400 indivíduos e que essa população dobra em um ano. A função que descreve esse crescimento é (assinale a alternativa correta):

TEXTO 6

Rápido, rápido

Sofro – sofri – de progéria, uma doença na qual o organismo corre doidamente para a velhice e a morte. Doidamente talvez não seja a palavra, mas não me ocorre outra e não tenho tempo de procurar no dicionário – nós, os da progéria, somos pessoas de um desmesurado senso de urgência. Estabelecer prioridades é, para nós, um processo tão vital como respirar. Para nós, dez minutos equivalem a um ano. Façam a conta, vocês que têm tempo, vocês que pensam que têm tempo. Enquanto isso, eu vou escrevendo aqui – e só espero poder terminar. Cada letra minha equivale a páginas inteiras de vocês. Façam a conta, vocês. Enquanto isso, e resumindo:

8h15min – Estou nascendo. Sou o primeiro filho – que azar! – e o parto é longo, difícil. Respiro, e já vou dizendo as primeiras palavras (coisas muito simples, naturalmente: mamã, papá) para grande surpresa de todos! Maior surpresa eles têm quando me colocam no berço – desço meia hora depois, rindo e pedindo comida! Rindo! Àquela hora,

8h45min – eu ainda podia rir.

9h20min – Já fui amamentado, já passei da fase oral – meus pais (ele, dono de um pequeno armazém; ela, de prendas domésticas) já aceitaram, ao menos em parte, a realidade, depois que o pediatra (está aí uma especialidade que não me serve) lhes explicou o diagnóstico e o prognóstico. E já estou com dentes! Em poucos minutos (de acordo com o relógio de meu pai, bem entendido) tenho sarampo, varicela, essas coisas todas.

Meus pais me matriculam na escola, não se dando conta que às 10h40min, quando a sineta bater para o recreio, já terei idade para concluir o primeiro grau. Vou para a escola de patinete; já na esquina, porém, abandono o brinquedo que parece-me então muito infantil. Volto-me, e lá estão os meus pais chorando, pobre gente.

10h20min – Não posso esperar o recreio; peço licença à professora e saio. Vou ao banheiro; a seiva da vida circula impaciente em minhas veias. Manipulo-me. Meu desejo tem nome: Mara, da oitava série. Por enquanto é mais velha do que eu. Lá pelas onze horas poderia namorá-la – mas então, já não estarei no colégio. Ali, me foge o doce pássaro da juventude.

[...]

(SCLIAR, Moacyr. Melhores contos. 6. ed. São Paulo: Global, 2003. p. 54-55.)

A

y = 400 × 2t.

B

y = 200 × 2t .

C

y = 100 × 2t .

D

y = 50 × 2t .

743c3a4e-b8

CEDERJ 2015 - Matemática - Aritmética e Problemas, Potenciação, Álgebra, Sistemas de Numeração e Operações Fundamentais, Radiciação, Funções, Equações Exponenciais

A alternativa que apresenta uma sentença verdadeira é:

A

O produto de dois números reais é sempre maior do que cada um dos fatores.

B

3^x > 2^x para todo valor real de x.

C

D

Se 0 < x < 1, então x² < x.

Questõessobre Equações Exponenciais