Questõessobre Equações Exponenciais

InícioTodas as questões
1
1
Foram encontradas 165 questões
fb1b0ec3-b4
UFJF 2016 - Matemática - Funções, Equações Exponenciais

A diferença entre o maior e o menor valor de x, na equação exponencial é igual a:

A
1
B
7
C
1/2
D
7/2
E
-3/2
e9b5de8e-b3
IF-MT 2016 - Matemática - Funções, Equações Exponenciais

A variável y , quando escrita em função de uma variável x , é dado por y= 5x-2 - 5. A variável x , portanto, quando escrita em função da variável y , é dada por


A
x=log5(5y)+2
B
x=log5(y+5)+2
C

x=1/25log5(y+5)

D

x=5y+5+2





E

abdcd13c-b3
IF-PR 2016 - Matemática - Funções, Equações Exponenciais

Encontre o domínio natural da função 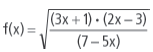(isto é, encontre todos os valores reais de x, para os quais

A

B

C

D

6ba59b96-b5
UFJF 2017 - Matemática - Funções, Equações Exponenciais

Durante o início de um experimento um pesquisador analisou uma população com 101 indivíduos. Após t anos a população passou a ser de 181 indivíduos, e depois de t² anos da análise inicial a população passou para 6661 indivíduos. A função y = bx + c com b > 1, determina o crescimento da população após x anos. Marque a alternativa contendo o valor da soma b + c.

A
103
B
104
C
109
D
110
E
111
65114681-d9
IF-RS 2018 - Matemática - Funções, Equações Exponenciais

Sabendo que f (x) = 2x e g (x) = 2-x , considere as afirmações abaixo.


I - f (x) + g (x) ≥ 2, para todo número real.

II - f (x) + g (x) = f (-x) + g (-x), para todo x número real.

III - se x > y então g (x) > g (y).


Assinale a alternativa correta.

A
É verdadeira somente a afirmação I.
B
É verdadeira somente a afirmação II.
C
São verdadeiras somente as afirmações I e II.
D
São verdadeiras somente as afirmações I e III.
E
São verdadeiras somente as afirmações II e III.
ebc32b36-dc
FAMEMA 2017 - Matemática - Funções, Equações Exponenciais, Função de 2º Grau

Os gráficos das funções f(x) = 1 + 2(x–k) e g(x) = 2x + b, com k e b números reais, se intersectam no ponto (3, 5). Sabendo que k e b são as raízes de uma função do 2o grau, a abscissa do vértice do gráfico dessa função é

A
1/2
B
-1
C
0
D
1
E
2
102c5801-d6
FEEVALE 2018 - Matemática - Função Modular, Funções, Função de 1º Grau, Equações Exponenciais, Função de 2º Grau

Considere os conjuntos , A = { ∎,⊗,Δ,*,⊚} , B = {1,2,3,4,5}  e a função f : A→ B definida pelos seguintes pares ordenados f= {(∎,1)}; (⊗,2); (Δ,3);(*,4);(⊚,5). Sobre essa função, são feitas as seguintes afirmações.


I- É uma função injetora, mas não é sobrejetora.

II- É uma função bijetora.

III- Essa função admite inversa f −1: B → A


Marque a alternativa correta.


 

A
Apenas a afirmação I está correta.
B
Apenas a afirmação II está correta.
C
Apenas a afirmação III está correta.
D
Apenas as afirmações I e II estão corretas.
E
Apenas as afirmações II e III estão corretas.
1020e33b-d6
FEEVALE 2018 - Matemática - Funções, Equações Exponenciais

Nos últimos anos, a população mundial aumentou substancialmente. Utilizam-se Funções Matemáticas exponenciais do tipo f(x) = ce kx , onde c > e k são constantes, para modelar tais fenômenos. Com relação a esse tipo de função, podemos afirmar que 

A
é uma função crescente somente para k > 0
B
é uma função crescente para qualquer valor de k.
C
é uma função decrescente somente para k > 0
D
é uma função que tem crescimento linear.
E
não existem funções exponenciais decrescentes.
252e0be7-e6
FAINOR 2019 - Matemática - Funções, Equações Exponenciais

Calcule o domínio da função

A
{x; 0 < x < 1}
B
{x; 1 < x < 2}
C
{x; x < 1 ou x > 2}
D
{x; x 0}
E
{x; x < 0 ou x > 1}
aae35f66-b5
UFBA 2013 - Matemática - Funções, Equações Exponenciais

De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) = (2x + 4) e x. Assim, é correto afirmar:


O gráfico de f tem concavidade voltada para cima.

C
Certo
E
Errado
aae620fa-b5
UFBA 2013 - Matemática - Funções, Equações Exponenciais

De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) = (2x + 4) e x. Assim, é correto afirmar:


Se o gráfico de f passa pelo ponto (0, 2), então também passa por (–1, –2).

C
Certo
E
Errado
aace7f92-b5
UFBA 2013 - Matemática - Funções, Equações Exponenciais

Na expressão y = 20e–x/2, y e x são, respectivamente, o preço unitário e a demanda mensal de um produto; logo a receita mensal auferida com a venda desse produto pode ser calculada pela fórmula R = 2y In (20/y).

C
Certo
E
Errado
aadda380-b5
UFBA 2013 - Matemática - Funções, Equações Exponenciais

De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) = (2x + 4) e x. Assim, é correto afirmar:

A função f é crescente no intervalo ]−∞ −, 2[ .

C
Certo
E
Errado
aac2e917-b5
UFBA 2013 - Matemática - Funções, Função de 1º Grau, Equações Exponenciais, Função de 2º Grau

Uma expressão algébrica da função f –1, inversa de f, é f –1 (x) = √3 (x – 2)

Para responder a essas questões, considere as funções f e g representadas nos gráficos, sabendo que

• o gráfico de f é uma reta que intersecta o eixo das ordenadas no ponto (0, 2) e faz com o eixo das abscissas um ângulo θ = π/3 rd  , adotando-se a mesma escala nos dois eixos coordenados;

• o gráfico de g é uma hipérbole que tem a reta x = 1 como assíntota vertical.

C
Certo
E
Errado
938599bc-db
FAMEMA 2018 - Matemática - Funções, Equações Exponenciais

Os gráficos das funções f(x) = 2x + k e g(x) = ax2 + bx, com k, a e b números inteiros, se intersectam no ponto (1, 1). Sabendo que g(2) = 0, o valor de g(f(3)) é

A
-3.
B
16.
C
-8.
D
8.
E
-16.
f7329fda-e2
UEPB 2011 - Matemática - Funções, Equações Exponenciais

A função f(x) = (m – 5 )x+1 é decrescente, quando:

A
4 < m < 6
B
5 < m < 6
C
0 < m < 6
D
5 < m < 7
E
m > 5
1cc17268-e2
UEPB 2011 - Matemática - Funções, Equações Exponenciais

A função f(x) = (m – 5 )x+1 é decrescente, quando:

A
m > 5
B
4 < m < 6
C
0 < m < 6
D
5 < m < 7
E
5 < m < 6
b489196d-e2
UEPB 2011 - Matemática - Funções, Equações Exponenciais

A função f(x) = (m – 5 )x+1 é decrescente, quando:

A
m > 5
B
4 < m < 6
C
0 < m < 6
D
5 < m < 7
E
5 < m < 6
7c5edfdb-df
UEPB 2009 - Matemática - Funções, Equações Exponenciais

Uma função real f é par se f(x) = f(–x) para todo x ∈ R. Se f(x) = x4 + px3 + x2 + qx for par, teremos necessariamente

A
p = q = 0
B
p = 0 e q ≠ 0
C
p ≠ 0 e q = 0
D
p + q = 1
E
p = –q
7c1fd35e-df
UEPB 2009 - Matemática - Funções, Equações Exponenciais

Se g e f são funções definidas por , com x ≠ –1, e f(x) = x −1 ,com x ≠ 0, então g(f(x)) é igual a:

A
f (g (x))
B
f (x)
C
g (x)
D
– g (x)
E
– f (x)