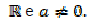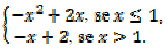e1e51978-b4
Unimontes - MG 2018 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau
Considere f : IR → IR uma função definida por

O esboço de gráfico que melhor representa a função f é
Considere f : IR → IR uma função definida por

O esboço de gráfico que melhor representa a função f é
A

B

C

D