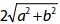Questõesde FGV sobre Função de 2º Grau

InícioTodas as questões
1
1
1
Foram encontradas 14 questões
0fbc533c-04
FGV 2020 - Matemática - Funções, Função de 2º Grau

Dadas as funções f(x) = x2 + 1 e g(x) = |x| + 1, ambas definidas para todos os números reais, o gráfico da função composta f(g(x)), em linha cheia, será

A

B

C

D

E

0fcf0129-04
FGV 2020 - Matemática - Funções, Função de 2º Grau

De acordo com o teorema fundamental da álgebra, quando resolvida em , a equação algébrica x4 – 3x3 + 2x2 – 6x = 0 possui quatro raízes. A respeito dessas raízes, pode-se afirmar que

A
duas são números irracionais e duas são números racionais positivos.
B
duas são números irracionais, uma é um número inteiro não negativo e a outra é um número racional não inteiro.
C
duas são números imaginários puros e duas são números inteiros não positivos.
D
duas são números imaginários puros e duas são números inteiros não negativos.
E
duas são números imaginários, uma é um número irracional e uma é número inteiro.
ba1ab285-fb
FGV 2012 - Matemática - Funções, Função de 2º Grau

O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.


Sobre os valores de a,b e c , tem-se:

A
a < 0, b > 0, c > 0
B
a < 0, b < 0, c > 0
C
a < 0, b < 0, c < 0
D
a > 0, b > 0, c < 0
E
a > 0, b > 0, c > 0
8aca5990-f3
FGV 2012, FGV 2012 - Matemática - Funções, Função de 2º Grau

O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.


Sobre os valores de a,b e c , tem-se:

A
a < 0, b > 0, c > 0
B
a < 0, b < 0, c > 0
C
a < 0, b < 0, c < 0
D
a > 0, b > 0, c < 0
E
a > 0, b > 0, c > 0
2dd34b1c-d8
FGV 2014 - Matemática - Funções, Função de 2º Grau

Para que valor de a , o conjunto imagem da função quadrática f(x) = ax2 -4x + 6 é o intervalo [−6, ∞[ ?

A
1/7
B
1/6
C
1/5
D
1/4
E
1/3
4bea820a-d7
FGV 2013 - Matemática - Funções, Função de 2º Grau

No plano cartesiano, há dois pontos R e S pertencentes à parábola de equação y=x2 e que estão alinhados com os pontos A(0,3) e B(4,0).

A soma das abscissas dos pontos R e S é: 

A
-0,45
B
-0,55
C
-0,65
D
-0,75
E
-0,85
1d4ac296-b0
FGV 2015 - Matemática - Funções, Função de 2º Grau

O comprimento do segmento determinado pelos pontos de intersecção das parábolas de equações

y = x2 - 8x + 3  e  y = -4x2 + 2x + 3 é:

A
2√37
B
3√41
C
7/2 √43
D
5/2 √39
E
4√45
1d280d85-b0
FGV 2015 - Matemática - Funções, Função de 2º Grau

Dada a função f(x) = x2 + 3, qual o valor da expressão

A
2x
B
2x + 1
C
2x - h
D
2x - 1
E
2x + h
3b1f83ca-9b
FGV 2017 - Matemática - Funções, Função de 2º Grau

O gráfico a seguir representa uma função real y = f(x) :



Das opções a seguir, aquela que pode representar a função dada é

A
y = x + 2
B
y = - x2 + x + 2
C
y = 6 - 4 . 2-x
D


E
y = 2 + In (x + 1)
6087be8d-1b
FGV 2015 - Matemática - Funções, Função de 2º Grau

O comprimento do segmento determinado pelos pontos de intersecção das parábolas de equações y = x2 - 8x + 3 e y = -4x2 + 2x + 3 é:

A
2√37
B
3√41
C


D


E
4√45
6063aa86-1b
FGV 2015 - Matemática - Funções, Função de 2º Grau

Dada a função f(x)= x2 + 3 , qual o valor da expressão

A
2 x
B
2x + 1
C
2x – h
D
2x – 1
E
2x + h
b24c4ea2-a6
FGV 2015, FGV 2015 - Matemática - Funções, Função de 2º Grau

A área de um segmento parabólico, sombreado na figura a seguir, pode ser calculada por meio da fórmula , sendo V o vértice da parábola.

                                       

Sendo b um número real positivo, a parábola de equação y = –0,5x2 + bx determina, com o eixo x do plano cartesiano, um segmento parabólico de área igual a 18. Sendo assim, b é igual a

A
2.
B
3.
C
4.
D
5.
E
6.
77ce435c-3d
FGV 2014 - Matemática - Funções, Função de 2º Grau

Seja f:IR →IR, tal que f(x)=x2+bx+15/4 , com b sendo uma constante real positiva.


Sabendo que a abscissa do ponto de mínimo do gráfico dessa função é igual a ordenada desse ponto, então, b é igual a

A
11/2
B
5
C
9/2
D
4
E
7/2
95c56970-fe
FGV 2014 - Matemática - Funções, Função de 2º Grau

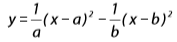Considere dois números reais a e b tais que a > b > 0 O gráfico da função corta o eixo das abscissas nos pontos P e Q. A distância entre P e Q é:

A
2( a + b )
B
2( a- b)
C
D
2ab/a+b
E
2√ab