Questõessobre Função de 2º Grau

InícioTodas as questões
1
1
Foram encontradas 425 questões
5885cc47-d7
MACKENZIE 2010 - Matemática - Álgebra, Funções, Função de 1º Grau, Produtos Notáveis e Fatoração, Função de 2º Grau

Considere f(x) = ax + b. Se f(0) = 1 e f(0) + f(1) + f(2) + ... + f(10) = –99, o valor de a3 + b3 é

A
-7
B
9
C
8
D
-4
E
-1
3ddbb254-d8
UEA 2019 - Matemática - Funções, Função de 2º Grau

Em um sistema de coordenadas cartesianas ortogonais estão representados os gráficos das funções f(x) e g(x), respectivamente, como uma reta e uma parábola de vértice V, que intercepta o eixo das abscissas no ponto M e na origem do sistema.




Sabendo-se que f(x) = 2x – 8 e que os pontos M e V são comuns aos dois gráficos, as coordenadas do vértice V são

A
(2, –4)
B
(2, –8)
C
(2, –6)
D
(3, –8)
E
(3, –6)
f49bf74b-d9
UFVJM-MG 2017 - Matemática - Funções, Função de 2º Grau

figura a seguir representa graficamente, no plano cartesiano, uma função de 2º grau f(x) = ax² + bx + c , em que a , b e c são constantes reais.



De acordo com a figura, a afirmação CORRETA é:

A
a c > 0.
B
b c < 0.
C
a b c < 0.
D
4 a c > b².
187e2e77-d8
INSPER 2015 - Matemática - Funções, Função de 2º Grau

Se as raízes x3 + 4x2 - 7x - 10 = 0 são -5, -1 e 2 então a soma dos quadrados das raízes da equação (x - 3)3 + 4(x-3)2 - 7(x-3) - 10 = 0 é igual a

A
16.
B
25.
C
29.
D
33.
E
41.
e54c2583-d9
UEA 2019 - Matemática - Funções, Função de 2º Grau

Sabe-se que o produto das raízes da função real f(x) = kx2 – 6kx + k + 7, com k ≠ 0, é igual a 8. Nessas condições, as coordenadas do vértice V da parábola definida pela função y = f(x) são

A
V (3, -2).
B
V(2, –1).
C
V (3, -1).
D
V (4, -1).
E
V(4, –2).
f676658d-d8
UERR 2015 - Matemática - Funções, Função de 2º Grau

O conjunto imagem da função f(x) = -x2 + 4, é

A
Im(f) = {y € IR / y ≤ 4}.
B
Im(f) = {y € IR / y > 4}.
C
Im(f) = {4}.
D
Im(f) = {y € IR / y ≥0}.
E
N.D.A.
a66e2451-d8
IFF 2016 - Matemática - Funções, Função de 2º Grau

Tadeu estava jogando vôlei com seus amigos. Em certo instante, ele fez um saque, e o movimento da bola foi semelhante ao gráfico de uma função quadrática com concavidade voltada para baixo. Considerando esse movimento, sabe-se que a altura máxima foi de 9 m e todo o percurso da bola foi realizado em 6 s. Se, no instante inicial e final, a bola estava na altura zero, então a altura no instante de 4 s é:

A
7 m.
B
8 m.
C
6 m.
D
5 m.
E
4 m.
2dd34b1c-d8
FGV 2014 - Matemática - Funções, Função de 2º Grau

Para que valor de a , o conjunto imagem da função quadrática f(x) = ax2 -4x + 6 é o intervalo [−6, ∞[ ?

A
1/7
B
1/6
C
1/5
D
1/4
E
1/3
4bea820a-d7
FGV 2013 - Matemática - Funções, Função de 2º Grau

No plano cartesiano, há dois pontos R e S pertencentes à parábola de equação y=x2 e que estão alinhados com os pontos A(0,3) e B(4,0).

A soma das abscissas dos pontos R e S é: 

A
-0,45
B
-0,55
C
-0,65
D
-0,75
E
-0,85
9d9452dc-d5
CESMAC 2017 - Matemática - Funções, Função de 2º Grau

A concentração C(x) de certo medicamento na corrente sanguínea, após x horas da sua ingestão, é dada por C(x) = -0,06x2 + 1,2x + 30, em partes por milhão (ppm). Parte do gráfico de C, para x real não negativo está esboçado a seguir:


Qual o valor máximo que a concentração do medicamento atinge?

A
33 ppm
B
34 ppm
C
35 ppm
D
36 ppm
E
37 ppm
fe6965e3-d1
UEA 2018 - Matemática - Funções, Função de 2º Grau

Sabe-se que o produto das raízes da função real f(x) = kx²– 6kx + k + 7, com k ≠ 0, é igual a 8. Nessas condições, as coordenadas do vértice V da parábola definida pela função y = f(x) são

A
V(3, –2).
B
V(2, –1).
C
V(3, –1).
D
V(4, –1).
E
V(4, –2).
87cea1aa-b6
IF-RS 2017 - Matemática - Análise de Tabelas e Gráficos, Funções, Função de 2º Grau

O gráfico abaixo representa a função f(x) = a + b.sen(x) .



Nessas condições, é correto afirmar que

A
a = -2 e b = 1
B
a = -1 e b = 2
C
a = 1 e b = -1
D
a = 1 e b = -2
E
a = 2 e b = -1
fd862b83-b4
UEFS 2010 - Matemática - Funções, Função de 2º Grau


Sabendo-se que todas as raízes do polinômio f(x), representadas graficamente na figura, são reais e que g-1(x) é a função inversa de g(x) = 2x – 1, pode-se concluir que o resto da divisão de f(x) por g-1(x) é

A
- 3
B
0
C
6
D
8
E
16
8f2f0893-b3
UFBA 2013 - Matemática - Funções, Função de 2º Grau

A função composta fog : R → R é tal que (fog)(x) = 1, para todo x ∈ R.

Sejam f : R → R e g : R → R as funções definidas, respectivamente, por f(x) = e g(x) = 

C
Certo
E
Errado
8f2c1d68-b3
UFBA 2013 - Matemática - Funções, Função de 2º Grau

f(–1) = 1 e g(5) = – 1.

Sejam f : R → R e g : R → R as funções definidas, respectivamente, por f(x) = e g(x) = 

C
Certo
E
Errado
8f292fad-b3
UFBA 2013 - Matemática - Funções, Função de 2º Grau

f(x) > 0, para todo x ∈] – 1, + ∞ [.

Considere a função real f(x) = x3 + x/x2 – 1.
C
Certo
E
Errado
8f21fdf7-b3
UFBA 2013 - Matemática - Funções, Função de 2º Grau

Pode-se afirmar que –1 ∈ D(f).

Considere a função real f(x) = x3 + x/x2 – 1.
C
Certo
E
Errado
8f25bd5e-b3
UFBA 2013 - Matemática - Funções, Função de 2º Grau

O gráfico de f intersecta a reta y = x + 1 em dois pontos distintos.

Considere a função real f(x) = x3 + x/x2 – 1.
C
Certo
E
Errado
a266e397-b2
UFRR 2017 - Matemática - Pontos e Retas, Geometria Analítica, Funções, Função de 2º Grau

Considerando a figura a seguir, assinale a alternativa que contém a equação da reta que corta a parábola nos pontos A e B.

A
y = 11/3 x + 1/3
B
y = x + 3
C
y = - 3x + 7
D
y = 3/5 x + 17/5
E
y = 4/3 x + 11/3
5403917e-b1
UFRR 2016 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

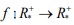Sejam dada por f (x) = 1/x e g : R → R dada por g (x) = 2x + 1. Encontre a área do quadrilátero ABCD, formado pelos pontos: A = (0,0), B = (0,g(0), C = 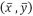, D = (1,0), onde 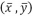é o ponto de intersecção dos gráficos de f e g, como ilustra a figura abaixo:



A
3/4 u.a;
B
5/4 u.a;
C
1/4 u.a;
D
2 u.a;
E
3 u.a.