Se a = −1, então ƒ○g (-1) = 3, em que
g : ℝ → ℝ é definida por g(x) = x − 1.




O custo de produção de um produto fabricado por uma cooperativa agrícola, em milhares de reais, é dado pela função C(x)= 4 + 6x, onde x é dado em milhares de unidades. Verificou-se que o faturamento de venda desses produtos, também em milhares de reais, é dado pela função F(x)= x2 + 3x. É correto afirmar que a cooperativa começará a ter lucro com a venda desse produto, a partir da produção de

O produto das coordenadas do ponto P, indicado na figura, é igual a
Considere a função

Sejam A e B subconjuntos não vazios
de  . Sejam f(A) = {f(a) / a
. Sejam f(A) = {f(a) / a  A} e f(B) =
{f(b) / b
A} e f(B) =
{f(b) / b  B} as imagens (diretas) de A e B
pela função f, respectivamente.
B} as imagens (diretas) de A e B
pela função f, respectivamente.
É correto afirmar que:
se A ∩ B = Φ, vale que f(A) ∩ f(B) = Φ.
se A  B; então vale que f(A)
B; então vale que f(A)  f(B).
f(B).
se f é crescente em A, vale que
y ≥ 0,  y ∈ f(A).
y ∈ f(A).
se B é o intervalo onde f é crescente e
positiva e f(A) ∩ f(B) = Φ, então A  [0,1].
[0,1].
FÍSICA - Formulário e Constantes
Um objeto é lançado do solo (origem) verticalmente para cima e retorna ao solo após k segundos. A altura que esse objeto se encontra do solo, em metros, em relação ao tempo t, em segundos, é dada pela função ƒ :[0,k] → ℝ definida por ƒ(t) = 40t − 5t2 em que ƒ(0) corresponde à sua altura no instante do lançamento. A esse respeito, considerando seus conhecimentos sobre Funções e sobre Cinemática e desprezando a resistência do ar, assinale o que for correto.
FÍSICA - Formulário e Constantes
Um objeto é lançado do solo (origem) verticalmente para cima e retorna ao solo após k segundos. A altura que esse objeto se encontra do solo, em metros, em relação ao tempo t, em segundos, é dada pela função ƒ :[0,k] → ℝ definida por ƒ(t) = 40t − 5t2 em que ƒ(0) corresponde à sua altura no instante do lançamento. A esse respeito, considerando seus conhecimentos sobre Funções e sobre Cinemática e desprezando a resistência do ar, assinale o que for correto.
Se a função f : R − {2} → R* é definida por 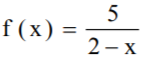 e f−1 a sua
inversa, então f -1 (-2) é igual a
e f−1 a sua
inversa, então f -1 (-2) é igual a
 para t ≥ 0.
para t ≥ 0.
{x ∈ Z; − 2 ≤ x < 3}

Sabendo que f(x) = 2x e g(x) = 2 -x , considere as afirmações abaixo.
I - f(x) + g(x) ≥ 2 , para todo número real.
II - f(x) + g(x) = f(-x) + g(-x), para todo x número real.
III- se , então x>y, então g(x) > g(y).
Assinale a alternativa correta.
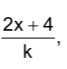 sendo k um número real não nulo. Sabendo que f(k) = 0, o
valor de f(g(4)) é
sendo k um número real não nulo. Sabendo que f(k) = 0, o
valor de f(g(4)) é