A curva obtida para o genótipo Aa, cuja frequência f é igual a
2pq, forma uma parábola que pode ser descrita, em função
de p, pela expressão:



Considere f : IR → IR uma função definida por

O esboço de gráfico que melhor representa a função f é




decrescente no intervalo 
crescente no intervalo 
decrescente no intervalo 
Assinale a afirmação incorreta referente à função f(x) =  , que tem como domínio e contradomínio o
conjunto dos números reais.
, que tem como domínio e contradomínio o
conjunto dos números reais.

O gráfico de f no intervalo (-6,6) é
Seja f : IR – { -1 } → IR uma função satisfazendo  para todo x real e diferente de 1 e de 0. Qual o valor
de f(tg2
α), para α real e α ≠ π/2 + kπ, k inteiro?
para todo x real e diferente de 1 e de 0. Qual o valor
de f(tg2
α), para α real e α ≠ π/2 + kπ, k inteiro?

O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.
Sobre os valores de a,b e c , tem-se:
O esboço de gráfico abaixo pode representar uma função ƒ: R-> R dada por

ƒ(x) = a² + 2, com a > 0
O gráfico a seguir representa uma função quadrática ƒ:R -> R definida por ƒ(x) = ax² + bx + c, com a, b, c em 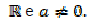 . Pode-se afirmar que
. Pode-se afirmar que

Considere ƒ : R -> R uma função definida por ƒ(x) =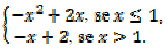 O esboço que representa o gráfico de ƒ é
O esboço que representa o gráfico de ƒ é





Dois números x e y que satisfazem a
equação  são:
são:

