Dada a função abaixo,

pode-se afirmar que o domínio da função f(x) é
Dada a função abaixo,

pode-se afirmar que o domínio da função f(x) é
Dada a função abaixo,

pode-se afirmar que o domínio da função f(x) é
Considere as duas funções reais f(x) e g(x), esboçadas no plano cartesiano abaixo.

Com base no gráfico, sabendo que
a = g(f(1)) - g (f(-1)), o valor de f(a + 1) é
A função quadrática tem diversas aplicações no nosso dia a dia. Na construção de antenas parabólicas, superfícies de faróis de carros e outras aplicações, são exploradas propriedades da parábola, nome dado à curva que é o gráfico de uma função quadrática.
Seja p(x)=mx2 +nx +1. Se p(2)=0 e p(–1)=0, então os valores de m e n são, respectivamente, iguais a
O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.
Sobre os valores de a,b e c , tem-se:
No gráfico a seguir estão representadas as funções R(x) e C(x) que indicam, respectivamente, a receita obtida na comercialização de x produtos de uma empresa e o custo de produção de tais produtos. Sabe-se que o custo fixo mensal da empresa é de R$ 2.800,00 e que cada unidade produzida gera um custo adicional de R$ 80,00.
Além disso, sabe-se que o lucro máximo na comercialização desses
produtos ocorre quando a diferença entre a receita e o custo de produção
é máxima (região representada no gráfico por 

No gráfico a seguir estão representadas as funções R(x) e C(x) que indicam, respectivamente, a receita obtida na comercialização de x produtos de uma empresa e o custo de produção de tais produtos. Sabe-se que o custo fixo mensal da empresa é de R$ 2.800,00 e que cada unidade produzida gera um custo adicional de R$ 80,00.
Além disso, sabe-se que o lucro máximo na comercialização desses
produtos ocorre quando a diferença entre a receita e o custo de produção
é máxima (região representada no gráfico por 

Considere as funções f(x) = 2x2 + 3 e g(x) = x - 5.
Quais são os valores reais de x tais que g(f(x))=0?
 x ∈
x ∈  .
. x ∈
x ∈  .
.Seja uma função real definida algebricamente pela expressão 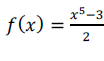 . Podemos
afirmar que a representação algébrica para f-1(x) será:
. Podemos
afirmar que a representação algébrica para f-1(x) será:











É correto afirmar sobre a função
quadrática  que:
que:
 é decrescente para
é decrescente para 
 possui três zeros diferentes.
possui três zeros diferentes.
 tem como vértice o ponto
tem como vértice o ponto
O valor máximo de
Para qual das funções abaixo, a
equação  não possui uma raiz real?
não possui uma raiz real?





Abaixo têm-se os gráficos das funções quadráticas f e g.

Sejam 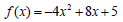 e
e 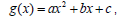 sabendo-se que a função f(x) intercepta o eixo das abscissas
nos pontos
sabendo-se que a função f(x) intercepta o eixo das abscissas
nos pontos 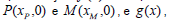 nos pontos (1,0) e
nos pontos (1,0) e 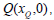 temos que g(2)=5. Se
g(x)
assume valor
máximo quando x=xm , conclui-se que xq é o valor do
parâmetro e
c
na função de
g(x)
são iguais a
temos que g(2)=5. Se
g(x)
assume valor
máximo quando x=xm , conclui-se que xq é o valor do
parâmetro e
c
na função de
g(x)
são iguais a