Questõessobre Função de 2º Grau
A parábola é uma curva que contém todos os pontos obtidos através de uma função. Assinale a alternativa que
representa esta função:
O consumo de combustível de um automóvel de competição em um trecho da pista varia em função da velocidade de acordo com a função C(v) = v2 + 3v, em que C é medido em km/l e v é a velocidade em m/s. Sabendo-se que a velocidade varia em função do tempo, através da função v(t) = 10 + t, em que t é medido em segundos, conclui-se que a função que representa o consumo de combustível, em função do tempo, é
Analise as afirmações:
I. Considerando x+y= 1 e x2 + y2=2, o valor de x3 + y3 é 5/2
II. Se 2 (22x) = 4x + 64 o valor de x3 = 27
III. No lançamento de dois dados, o percentual do produto dos números obtidos nos dois dados ser divisível por 2 e 3 simultaneamente é de aproximadamente 41,7%.
IV. Suponha que os gráficos de f(x)= x2 e g(x)=2x sejam feitos sobre uma malha coordenada quadriculada onde a unidade de comprimento seja 1cm. A distância de 0,12m à direita da origem, a altura do gráfico de f é um pouco maior do que 1 m e a altura do gráfico de g é maior do que a altura de um prédio de 15 andares ao considerar um pé-direito de 2,5 m ( altura padrão entre o piso e o teto.Está correto o que se afirma em:
Analise as afirmações:
Está correto o que se afirma em:
Analise as afirmações:
I. O domínio da função f(x) = 1/x2-x é dado por {x|≠x0,x≠1}
II. Uma curva no plano XY é o gráfico de uma função de x se e somente se nenhuma reta vertical cortar a curva mais de uma vez.
III. Se f(x) = x2 + 2x - 1 e g(x) = 2x - 3, então f[g(x)] = x2 - 8x +2
IV. Dada f(x)=  então f(-2) + f(1) = 3
então f(-2) + f(1) = 3
Está correto o que se afirma em:
Analise as afirmações:
I. O domínio da função f(x) = 1/x2-x é dado por {x|≠x0,x≠1}
II. Uma curva no plano XY é o gráfico de uma função de x se e somente se nenhuma reta vertical cortar a curva mais de uma vez.
III. Se f(x) = x2 + 2x - 1 e g(x) = 2x - 3, então f[g(x)] = x2 - 8x +2
IV. Dada f(x)=  então f(-2) + f(1) = 3
então f(-2) + f(1) = 3
Está correto o que se afirma em:
Se a função ݂: f :ℝ - { 2 } → ℝ é definida por ݂f (x) = 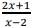 e a
função ݃ g :ℝ - { 2 } → ℝ é definida por ݃g (x) = f ( f(x) ), então
݃g(x) é igual a
e a
função ݃ g :ℝ - { 2 } → ℝ é definida por ݃g (x) = f ( f(x) ), então
݃g(x) é igual a
Se a função ݂: f :ℝ - { 2 } → ℝ é definida por ݂f (x) = 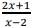 e a
função ݃ g :ℝ - { 2 } → ℝ é definida por ݃g (x) = f ( f(x) ), então
݃g(x) é igual a
e a
função ݃ g :ℝ - { 2 } → ℝ é definida por ݃g (x) = f ( f(x) ), então
݃g(x) é igual a
Analise as afirmações:
I-O domínio da função f(x)= 1/x2 + 1 é dado por todos os números reais.
II-Dada g(x) =  , o valor de g(-2) = 18
, o valor de g(-2) = 18
III-Se f(x)= x2 e g(x)=2x, então f [g(x)]=2g[f(x)]
IV- A solução da inequação |x+2| + |4−2x|<7 é S = {x E ℝ|−1<x<3}
É incorreto o que afirma em:
Analise as afirmações:
I-O domínio da função f(x)= 1/x2 + 1 é dado por todos os números reais.
II-Dada g(x) =  , o valor de g(-2) = 18
, o valor de g(-2) = 18
III-Se f(x)= x2 e g(x)=2x, então f [g(x)]=2g[f(x)]
IV- A solução da inequação |x+2| + |4−2x|<7 é S = {x E ℝ|−1<x<3}
É incorreto o que afirma em:
No lançamento de uma bola de basquete, a trajetória é parabólica.
Considere um arremesso no qual o atleta se encontra há 6 metros (distância horizontal) da cesta, conforme a figura abaixo:

No lançamento descrito acima, a altura máxima atingida pela bola, em
metros, foi de:

No lançamento descrito acima, a altura máxima atingida pela bola, em
metros, foi de:
Dada a função: f(x) = 6x² - x -1 , analise as proposições e assinale a alter
I.O domínio de f(x): ; d = { x ∈ R };
II. A imagem de f(x): ; I = {y - ∈ R|y ≥ -25/24};
III. A imagem de f(x): nativa verdadeira. I = {y - ∈ R| -1/3 ≤ y ≤ 1/2};
Dada a função: f(x) = 6x² - x -1 , analise as proposições e assinale a alter
I.O domínio de f(x): ; d = { x ∈ R };
II. A imagem de f(x): ; I = {y - ∈ R|y ≥ -25/24};
III. A imagem de f(x): nativa verdadeira. I = {y - ∈ R| -1/3 ≤ y ≤ 1/2};
No plano cartesiano a seguir, estão esboçados os gráficos das
funções f(x) = x2 – 2x e g(x) = x.

Sabendo-se que A e C referem-se aos pontos de interseção
entre os gráficos das funções f e g, a área do triângulo ABC, em
unidades de área, é:
No plano cartesiano a seguir, estão esboçados os gráficos das funções f(x) = x2 – 2x e g(x) = x.
Sabendo-se que A e C referem-se aos pontos de interseção
entre os gráficos das funções f e g, a área do triângulo ABC, em
unidades de área, é:
Considere as funções ƒ(x) = x2 + 4 e g(x) = 1 + log½ x,
em que o domínio de ƒ é o conjunto dos números reais e o
domínio de g é o conjunto dos números reais maiores do
que 0. Seja
h(x) = 3ƒ(g(x)) + 2g(ƒ(x)),
em que x > 0. Então, h(2) é igual a
Considere as funções ƒ(x) = x2 + 4 e g(x) = 1 + log½ x, em que o domínio de ƒ é o conjunto dos números reais e o domínio de g é o conjunto dos números reais maiores do que 0. Seja
h(x) = 3ƒ(g(x)) + 2g(ƒ(x)),
em que x > 0. Então, h(2) é igual a
Considere as funções f(x) = x2/2 + b e g(x)= x + k, com b e k, números reais.
• Sabendo que
f(g(-5)) = g(-2) e que g(f(-2)) = 12, o valor de f(-4)
é igual a
Considere as funções f(x) = x2/2 + b e g(x)= x + k, com b e k, números reais.
• Sabendo que
f(g(-5)) = g(-2) e que g(f(-2)) = 12, o valor de f(-4)
é igual a
Todas as proposições a seguir estão corretas, exceto a
O domínio da função  é o
conjunto dos números reais.
é o
conjunto dos números reais.
Dadas as funções:

Então, o valor de h(ƒ(g(4))) é 6.
Um objeto foi lançado para cima de uma altura de 3 metros em
relação ao solo. Sua trajetória até o solo é parabólica e está descrita no gráfico.

Durante a trajetória, o objeto esteve a exatos 2 metros de altura
em relação ao solo após t segundos do lançamento. Sendo assim,
t é igual a

É correto afirmar que o valor de k para que a função f(x)=x2 - 2x + k tenha o valor mínimo 2 é
Uma bolinha é lançada no ar, e sua altura , em metros, após t segundos do lançamento é
dada pela função h(t) = -t² +4t + 6. Qual das alternativas representa a altura máxima
atingida por essa bolinha?
Considere a função f(x) = √x - 7. Sobre essa função são feitas as seguintes afirmativas:
I. O conjunto de maior domínio dessa função é dado por D (F) = { x ∈ R/ x ≥ 7 };
II.f (11) = 2;
III. A função está definida para qualquer valor de x real
Assinale a alternativa CORRETA.
Considere a função f(x) = √x - 7. Sobre essa função são feitas as seguintes afirmativas:
I. O conjunto de maior domínio dessa função é dado por D (F) = { x ∈ R/ x ≥ 7 };
II.f (11) = 2;
III. A função está definida para qualquer valor de x real
Assinale a alternativa CORRETA.
Uma estufa tem a forma de uma parábola como
representado a seguir.

A estufa tem 8 m de largura no nível do solo, e sua
altura máxima é de 2,4 m. Existem dois postes de
sustentação da estufa que se encontram a uma
distância de 2 m de cada lado. Qual a altura dos
postes?
