Assinale a proposição CORRETA.
Para a função  , a área da região limitada pelos eixos
coordenados (x = 0 e y = 0) e pelo gráfico de ƒ, é 8,5 unidades de área.
, a área da região limitada pelos eixos
coordenados (x = 0 e y = 0) e pelo gráfico de ƒ, é 8,5 unidades de área.
Assinale a proposição CORRETA.
Para a função  , a área da região limitada pelos eixos
coordenados (x = 0 e y = 0) e pelo gráfico de ƒ, é 8,5 unidades de área.
, a área da região limitada pelos eixos
coordenados (x = 0 e y = 0) e pelo gráfico de ƒ, é 8,5 unidades de área.

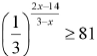 . O conjunto formado por
todos os números reais que satisfazem essa inequação é:
. O conjunto formado por
todos os números reais que satisfazem essa inequação é:
 então o conjunto imagem de f é
então o conjunto imagem de f é 







