Questõessobre Função de 1º Grau
Define-se o erro da função f para o ponto (x,y) como sendo o valor \ f(x) —y\ e o erro de f para o conjunto de pontos
C como sendo a soma dos erros de f para todos os pontos de C. Entre as funções abaixo, qual possui o menor erro
para o conjunto C = {(0,5), (1,3), (2, —1)}?
Considere ƒ : R -> R uma função definida por ƒ(x) =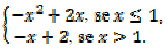 O esboço que representa o gráfico de ƒ é
O esboço que representa o gráfico de ƒ é
Considere ƒ : R -> R uma função definida por ƒ(x) =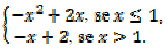 O esboço que representa o gráfico de ƒ é
O esboço que representa o gráfico de ƒ é




Um livro é vendido por R$ 30,00 a unidade e o custo para produzir cada livro corresponde a um valor fixo de R$ 5,00
mais R$ 10,00 por unidade. Nessas condições, pode-se afirmar que o lucro obtido na venda de x livros é, em reais,
dado por uma função afim ƒ, definida por
Considerem-se os valores registrados na tabela T, obtidos em certo
experimento, que foram relacionados por meio de funções reais,
bijetoras, f e g.

Analisando-se as informações contidas em T, pode-se concluir que a
relação entre a e b é expressa por

O conjunto-solução da inequação  é um subconjunto de
é um subconjunto de
O conjunto-solução da inequação  é um subconjunto de
é um subconjunto de
Considere o gráfico da função f(x) = x5
para os cálculos desta
questão.

A cafeína é eliminada da corrente sanguínea de um adulto a
uma taxa de, aproximadamente, 15% por hora. Cinco horas
após o consumo de um café expresso, que contém 200 mg
de cafeína, um adulto ainda terá em sua corrente sanguínea
a quantidade aproximada de cafeína de
Considere o gráfico da função f(x) = x5 para os cálculos desta questão.

A cafeína é eliminada da corrente sanguínea de um adulto a
uma taxa de, aproximadamente, 15% por hora. Cinco horas
após o consumo de um café expresso, que contém 200 mg
de cafeína, um adulto ainda terá em sua corrente sanguínea
a quantidade aproximada de cafeína de
Seja f: R ↠ R, tal que, para todo x ∈ R, f(3 x) = 3 f (x). Se f (9) = 45, então f (1) é igual a:
Uma função real f(x) satisfaz às condições: f(x + y) = f(x) + f(y) para
todo x e y reais, f(1) = 3 e f (√5 ) = 4. O valor de f (2 + √5) é:
Se f (x) = (2 x + 1)/(x - 2) , então, f [f( - 3)] vale
Seja a função definida por f(x) = (x + 1)/(4x + 1), x ≠ -1/4 e f-1 = (-x + 1)/(ax + b). A soma (a + b) é
Considerando a função real definida por
y = 1 + cos2x, pode-se afirmar que
O valor arrecadado com a venda de um
produto depende da quantidade de unidades
vendidas.
A tabela abaixo apresenta alguns exemplos de arrecadação ou receita.

Com base nos dados da tabela, a função que
melhor descreve a arrecadação é a

Considere as funções h : ℝ → ℝ, definida por
h(x) = kx + 3, com k ∈ ℝ, e s: ℝ → ℝ, tal que
s(x) = ƒ(x) + h(x). Se o gráfico da função s
tem vértice na origem do sistema cartesiano,
então a = k.

Supondo que a função ƒ: ℕ → ℕ definida por ƒ(n) = 2 + 4n, represente o comprimento total
(em milímetros) de uma unha humana após
n meses, então pode-se estimar que, após 25
anos, sem qualquer interferência nesse
processo de crescimento, as unhas teriam
102 mm de comprimento.

Os itens a seguir referem-se ao processo contínuo de reconstrução dos organismos vivos. Assinale o que for correto.
Considere uma função f(x), cujo gráfico está
desenhado ao lado:

O gráfico que representa a função g(x) = f(x+1) + f(x-1) é:
Considere uma função f(x), cujo gráfico está desenhado ao lado:

O gráfico que representa a função g(x) = f(x+1) + f(x-1) é:





A figura abaixo apresenta o gráfico de uma função y = f(x) .

A partir das informações contidas no gráfico, marque V para as
afirmativas verdadeiras e F para as falsas.
( ) f(x) é uma função injetora.
( ) O domínio de ) f(x é o intervalo ]− 2;3] .
( ) f(x) = 2 , para todo 2 ≤ x ≤ 4 .
( ) f(x) ≥ 0 , para 
Assinale a seqüência correta.
A figura abaixo apresenta o gráfico de uma função y = f(x) .

A partir das informações contidas no gráfico, marque V para as afirmativas verdadeiras e F para as falsas.
( ) f(x) é uma função injetora.
( ) O domínio de ) f(x é o intervalo ]− 2;3] .
( ) f(x) = 2 , para todo 2 ≤ x ≤ 4 .
( ) f(x) ≥ 0 , para 
Assinale a seqüência correta.
Dada a função f (x) = ax + b, sendo a, b constantes
reais e sabendo-se que f (2) = 5 e f ( 1) = 4, é
correto afirmar que
Considerando a função f, de variável real definida
por f(x) = 3 - x + k(x-1) , pode-se afirmar
que
A solução da inequação |3x + 9| <12 é o conjunto




