11993b58-f5
UFRN 2012 - Matemática - Funções, Função de 2º Grau
A pedido do seu orientador, um bolsista de um laboratório
de biologia construiu o gráfico ao lado a partir dos dados
obtidos no monitoramento do crescimento de uma cultura
de micro-organismos.
Analisando o gráfico, o bolsista informou ao orientador que a
cultura crescia segundo o modelo matemático, N - K. 2 AT,
com t em horas e N em milhares de micro-organismos.
Para constatar que o modelo matemático apresentado pelo
bolsista estava correto, o orientador coletou novos dados
com t=4 horas e t= 8 horas.
Para que o modelo construído pelo bolsista esteja correto,
nesse período, o orientador deve ter obtido um aumento na
quantidade de micro-organismos de

A pedido do seu orientador, um bolsista de um laboratório
de biologia construiu o gráfico ao lado a partir dos dados
obtidos no monitoramento do crescimento de uma cultura
de micro-organismos.
Analisando o gráfico, o bolsista informou ao orientador que a
cultura crescia segundo o modelo matemático, N - K. 2 AT,
com t em horas e N em milhares de micro-organismos.
Para constatar que o modelo matemático apresentado pelo
bolsista estava correto, o orientador coletou novos dados
com t=4 horas e t= 8 horas.
Para que o modelo construído pelo bolsista esteja correto,
nesse período, o orientador deve ter obtido um aumento na
quantidade de micro-organismos de

A
80.000.
B
160.000.
C
40.000.
D
120.000.

 para t
para t 
 , com
, com  em horas e N em milhares de micro-organismos.
em horas e N em milhares de micro-organismos. 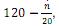 , onde
, onde 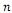 é o número de uniformes comprados, com o valor por uniforme se tornando constante a partir de 500 unidades.
é o número de uniformes comprados, com o valor por uniforme se tornando constante a partir de 500 unidades.  são paralelas entre si.
são paralelas entre si. 
 e quer ir para a rua
e quer ir para a rua  até à posição B.
até à posição B. para t ≥ 0 .
para t ≥ 0 .  é maior que o de
é maior que o de  .
. é menor que o de
é menor que o de 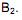 .
. aumenta 10% e o de
aumenta 10% e o de  aumenta 90%.
aumenta 90%. cresce 20 vezes menos que o de
cresce 20 vezes menos que o de  .
.