Questõesde UFRGS sobre Funções

InícioTodas as questões
1
1
1
Foram encontradas 20 questões
9428d9d0-05
UFRGS 2016 - Matemática - Funções, Equações Exponenciais

Considere a função f definida por f (x) = 1- 5 . 0,7x e representada em um sistema de coordenadas cartesianas.

Entre os gráficos abaixo, o que pode representar a função f é

A

B

C

D

E

9425ef0a-05
UFRGS 2016 - Matemática - Funções, Logaritmos

Se 10x = 20y, atribuindo 0,3 para log 2, então o valor de x/y é

A
0,3.
B
0,5.
C
0,7.
D
1.
E
1,3.
cf0b72b3-fa
UFRGS 2019 - Matemática - Funções, Função de 1º Grau

Considere as funções f(x) = |x + 1| e g(x) = - |x| - 1.


O intervalo tal que f(x) > g(x) é

A
(- ∞, - 1) U (1, + ∞).
B
(-1/2, 1/2).
C
(- ∞, 0) U (1, + ∞).
D
(-1, + ∞).
E
(- ∞, + ∞).
cf213780-fa
UFRGS 2019 - Matemática - Funções, Função de 1º Grau

O gráfico de f(x) = x3 está representado na imagem a seguir.



O esboço do gráfico de g(x) = x³ + 3x² + 3x + 1 está representado na alternativa

A

B

C


D

E

cf1cdd41-fa
UFRGS 2019 - Matemática - Funções, Logaritmos

Se log 2 = x e log 3 = y, então log 288 é

A
2x + 5y.
B
5x + 2y.
C
10xy.
D
x² + y².
E
x² - y².
eb508a50-af
UFRGS 2017 - Matemática - Funções, Função de 2º Grau

Dadas as funções ƒ e g , definidas por ƒ(x)= x2 + 1 e g(x) = x , o intervalo tal que ƒ(x) > g(x) é

A

B

C

D

E
(-∞ , +∞).
eb54f2ad-af
UFRGS 2017 - Matemática - Funções, Função de 2º Grau

Considere a função y = ƒ(x) representada no sistema de coordenadas cartesianas abaixo.



O gráfico que pode representar a função y = |ƒ(x + 2) +1 é

A

B

C

D

E

eb45e4f0-af
UFRGS 2017 - Matemática - Funções, Logaritmos

Se log5 x = 2 e log10 y = 4 , então log20 y/x é

A
2.
B
4.
C
6.
D
8.
E
10.
d1164e95-ba
UFRGS 2019 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

O gráfico de ƒ(x) está esboçado na imagem a seguir.



O esboço do gráfico de |ƒ(x − 3)| + 2 está representado na alternativa

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A

B


C


D


E


d111f59b-ba
UFRGS 2019 - Matemática - Função Logarítmica, Funções

O valor d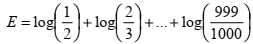e


é .

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A
− 3 .
B
− 2 .
C
− 1 .
D
0.
E
1.
d124bc5f-ba
UFRGS 2019 - Matemática - Funções, Função de 1º Grau

Considere a função real de variável real ƒ(x) = 3 - 5sen (2x + 4). Os valores de máximo, mínimo e o período de ƒ(x) são, respectivamente,

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A
-2, 8, π.
B
8, -2, π.
C
π, -2, 8.
D
π, 8, -2.
E
8, π, -2.
d10d5ad4-ba
UFRGS 2019 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

Considere a função real de variável real ƒ(x) = 2x -1 . Com relação à ƒ(x ), é correto afirmar que

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A
se x < 1, então ƒ(x) < 0 .
B
se x ≥ 1, então ƒ(x) ≤ 1 .
C
a função ƒ(x) é decrescente para x < 0 e crescente para x ≥ 0 .
D
os valores das imagens de ƒ ( x ) : A → R , em que A = { x ∈ N / x ≥ 0 } , formam uma progressão aritmética.
E
os valores das imagens de ƒ ( x ) : A → R , em que A = { x ∈ N / x ≥ 0 } , formam uma progressão geométrica.
d105397c-ba
UFRGS 2019 - Matemática - Função Logarítmica, Funções

Dadas as funções reais de variável real ƒ e g , definidas por ƒ(x) = −log2 (x) e g(x) = x2 − 4 , pode-se afirmar que ƒ(x) = g(x) é verdadeiro para um valor de x localizado no intervalo

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A
[0; 1].
B
[1; 2].
C
[2; 3].
D
[3; 4].
E
[4; 5].
d1013992-ba
UFRGS 2019 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

Considere as seguintes afirmações sobre quaisquer funções ƒ reais de variável real.


I - Se x ∈ R e x > 0, então ƒ(x) > 0 .

II - Se ƒ(x) = 0 , então x é zero da função ƒ(x).

III- Se x1 e x2 são números reais, com x1 < x2 , então ƒ( x1) < ƒ(x2) .


Quais estão corretas?

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A
Apenas I.
B
Apenas II.
C
Apenas III.
D
Apenas I e II.
E
I, II e III.
77077a9e-cc
UFRGS 2018 - Matemática - Funções, Função de 1º Grau

A representação geométrica das retas r e s encontra-se desenhada no sistema de coordenadas cartesianas na imagem a seguir.



Assinale a alternativa que apresenta o sistema de equações lineares que pode representar as retas r e s da imagem acima.

A


B


C


D


E


76d6202a-cc
UFRGS 2018 - Matemática - Funções, Logaritmos

Se log3x + log9x = 1, então o valor de x é

A
∛2.
B
√2.
C
∛3.
D
√3.
E
∛9.
76dd4a73-cc
UFRGS 2018 - Matemática - Funções, Logaritmos

Leia o texto abaixo, sobre terremotos.


Magnitude é uma medida quantitativa do tamanho do terremoto. Ela está relacionada com a energia sísmica liberada no foco e também com a amplitude das ondas registradas pelos sismógrafos. Para cobrir todos os tamanhos de terremotos, desde os microtremores de magnitudes negativas até os grandes terremotos com magnitudes superiores a 8.0, foi idealizada uma escala logarítmica, sem limites. No entanto, a própria natureza impõe um limite superior a esta escala, já que ela está condicionada ao próprio limite de resistência das rochas da crosta terrestre. Magnitude e energia podem ser relacionadas pela fórmula descrita por Gutenberg e Richter em 1935: log(E) = 11,8 + 1,5 M onde: E = energia liberada em Erg ; M = magnitude do terremoto.

Disponível em:<http://www.iag.usp.br/siae98/terremoto/terremotos.htm >. Acesso em: 20 set. 2017.


Sabendo que o terremoto que atingiu o México em setembro de 2017 teve magnitude 8,2, assinale a alternativa que representa a melhor aproximação para a energia liberada por esse terremoto, em Erg .

A
13,3
B
20
C
24
D
1024
E
1028
76c6b9d7-cc
UFRGS 2018 - Matemática - Funções, Função de 2º Grau

As raízes da equação 2x2 + bx + c = 0 são 3 e − 4. Nesse caso, o valor de b - c é

A
−26.
B
−22.
C
−1.
D
22.
E
26.
76cea5d2-cc
UFRGS 2018 - Matemática - Funções, Função de 1º Grau

Considere a função real ƒ definida por ƒ(x) =2-x . O valor da expressão S = ƒ(0) + ƒ(1) + ƒ(2) + ... + ƒ(100) é

A
S = 2 - 2-101.
B
S = 250 + 2-50.
C
S = 2 + 2-101.
D
S = 2 + 2-100.
E
S = 2 - 2-100.
76bf2e2b-cc
UFRGS 2018 - Matemática - Funções, Função de 2º Grau

Dadas as funções reais de variável real ƒ e g, definidas por ƒ(x) = x3 e g (x) = ∛x , o intervalo, tal que ƒ(x) > g (x) , é

A
(0; +∞)
B
(-∞; -1) ∪ (0; 1).
C
(-1; 1).
D
(-∞; -1) ∪ (1; +∞).
E
(-1; 0) ∪ (1; +∞).