Na figura, os segmentos OR e PQ são lados paralelos do quadrilátero
OPQR, e o vértice Q é o ponto em que a função f(x) = 2(−x2 + 4x) assume
seu maior valor.

Sendo a área da região sombreada igual a 18u.a., pode-se afirmar que
uma equação cartesiana da reta r que contém o lado RQ do
quadrilátero é

 é um subconjunto de
é um subconjunto de
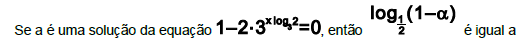



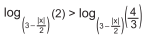 é um subconjunto de
é um subconjunto de


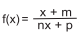 , para − 1 ≤ x ≤ 3,
pode-se afirmar corretamente que o valor de (n − m).p é
, para − 1 ≤ x ≤ 3,
pode-se afirmar corretamente que o valor de (n − m).p é
 .
.










