d6c37e1a-a6
UECE 2010 - Matemática - Funções, Logaritmos
Se f(x) =  defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por
defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por
{ y ∈ R ; = g (x) , x ≠ 0 } , é
Se f(x) =  defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por
defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por
{ y ∈ R ; = g (x) , x ≠ 0 } , é
 defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por
defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por { y ∈ R ; = g (x) , x ≠ 0 } , é
A
( - ∞,0 ].
B
( - ∞,1 ] .
C
[ 0 , + ∞) .
D
[ 1 , + ∞ ) .
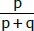 é
é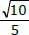
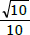
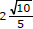
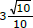
 então o valor da soma
então o valor da soma 
 existe um único número
existe um único número tal que para exatamente três números
tal que para exatamente três números  verifica-se a relação
verifica-se a relação  Nestas condições o valor da soma
Nestas condições o valor da soma 
 = k podemos afirmar, corretamente, que a soma das raízes da equação 2x - 12 + 27.2 -x = 0 é igual a
= k podemos afirmar, corretamente, que a soma das raízes da equação 2x - 12 + 27.2 -x = 0 é igual a  formam, nesta ordem, uma progressão aritmética, com
formam, nesta ordem, uma progressão aritmética, com  então o valor de
então o valor de 