b47365d2-b6
UECE 2010 - Matemática - Funções, Equação Logarítmica
Se os números m, p e q são as soluções da equação
x
3 – 7x2 + 14x – 8 = 0 então o valor da soma
log2m + log2p + log2q é
Se os números m, p e q são as soluções da equação
x
3 – 7x2 + 14x – 8 = 0 então o valor da soma
log2m + log2p + log2q é
A
1.
B
2.
C
3.
D
4.
 é a função real de variável
real definida por f(x) = e
é a função real de variável
real definida por f(x) = e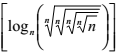 é
é
 é invertível. Se f
é invertível. Se f