Questõesde UDESC sobre Funções
A Figura 1 representa o gráfico da função 

A solução da inequação 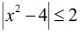 é dada por:
é dada por:
A Figura 1 representa o gráfico da função 

A solução da inequação 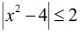 é dada por:
é dada por:





Considere a sequência 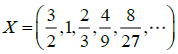 . Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
. Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
Considere a sequência 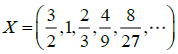 . Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
. Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
Define-se como função exponencial a relação dada por
f :
R → R tal que f (x)= ax , sendo
a∈R , a > 0
e
a ≠1.
Analise as sentenças, e assinale (V) para verdadeira e (F) para falsa.
( )f (x)=2-x não é uma função exponencial.
( ) Uma função exponencial não está definida para valores negativos de
x .
( ) f( x) = πx é uma função exponencial e intercepta o eixo das ordenadas em y =1.
( ) Toda função exponencial possui uma assíntota horizontal.
Define-se como função exponencial a relação dada por f : R → R tal que f (x)= ax , sendo a∈R , a > 0 e a ≠1. Analise as sentenças, e assinale (V) para verdadeira e (F) para falsa.
( )f (x)=2-x não é uma função exponencial.
( ) Uma função exponencial não está definida para valores negativos de x .
( ) f( x) = πx é uma função exponencial e intercepta o eixo das ordenadas em y =1.
( ) Toda função exponencial possui uma assíntota horizontal.
Considerando ln 10 = 2,3, então o valor da expressão  é igual a:
é igual a:
Considerando ln 10 = 2,3, então o valor da expressão  é igual a:
é igual a:
Uma circunferência tem o seu raio variando de acordo com a imagem da função f : [2,6] —» ℜ, onde f (x) = -1/2 x2 + 3x + 4. A diferença entre o maior e o menor comprimento possível dessa circunferência é de:
O conjunto solução da inequação 
O conjunto solução da inequação 







Uma função
f
é dita par se para todo
x
do domínio tem-se que
f(-x) = f(x), e uma
função
g
é dita ímpar se para todo
x
do domínio tem-se que
g(-x) = -g(x).
Sobre essas informações, analise as sentenças.
I. O gráfico de uma função ímpar é simétrico em relação à origem do sistema cartesiano.
II. O gráfico de uma função par é simétrico em relação à origem do sistema cartesiano.
III. O gráfico de uma função ímpar é simétrico em relação ao eixo das ordenadas.
IV. O gráfico de uma função par é simétrico em relação ao eixo das ordenadas.
V. Os gráficos das funções pares e ímpares possuem a mesma simetria.
Das sentenças acima, tem-se exatamente:


Sejam
f
e
g
as funções definidas por
 e
e  Se A é o conjunto que
representa o domínio da função
f
e
Se A é o conjunto que
representa o domínio da função
f
e  , então o conjunto
, então o conjunto 
Sejam f e g as funções definidas por
 e
e  Se A é o conjunto que
representa o domínio da função
f
e
Se A é o conjunto que
representa o domínio da função
f
e  , então o conjunto
, então o conjunto 





Sejam a e b números naturais para os quais log(a+1)
(b + 2a) = 2 e 1+ loga
( b - 1) = a.
Então log3a (3b - a) é igual a:
Sejam a e b números naturais para os quais log(a+1) (b + 2a) = 2 e 1+ loga ( b - 1) = a.
Então log3a (3b - a) é igual a:
Considere os valores de x pertencentes ao conjunto S = { x ∈ R/ x > - 4}. Associe cada uma das funções f (x) com x ∈ S,exibidas na coluna A da Tabela 1 com as suas respectivas inversas, exibidas na coluna B.
Tabela 1: Funções e suas inversas A B (1) f(x) = log2 4√x + 4 ( ) f-1(x) = (√2) x+4- 4
(2) f(x) = 2 log2( x+4/4) ( ) f-1 (X) = 22x-1 - 4
(3) f(x) = log4(2x + 8) ( ) f-1 (x) = 24x - 4
Assinale a alternativa que contém a sequência correta de classificação, de cima para baixo.
Uma maneira de calcular, aproximadamente, a área de uma região abaixo do gráfico de uma
função é inscrever retângulos de bases iguais nesta região, de modo que a base dos
retângulos esteja sobre o eixo x e um dos vértices de cada retângulo sobre o gráfico da função.
Usando esta técnica, quanto maior for o número de retângulos melhor será a aproximação da
área da região abaixo do gráfico da função. A Figura 1 é um exemplo do uso desta técnica para
calcular, aproximadamente, a área abaixo do gráfico da função f (x) = x2 no intervalo [a,b].

Figura 1: Aproximação da área
Usando a técnica descrita acima, a área aproximada abaixo do gráfico da função g (x) = x2 / 4 + x + 1 no intervalo [0, 10], usando cinco retângulos será de:

Os gráficos das funçõesf (x) = 1 -x, g(x) = 6x e h(x) = -x2 + 2x + 5 estão ilustrados na Figura 1.

Analise as sentenças abaixo, em relação às informações anteriores.
I. f(x) ≤ h(x) ≤ g(x) se, e somente se, 1 ≤ x ≤ 4
II. f(x) ≤ h(x) ≤ g(x) se, e somente se, 0 ≤ x ≤ 4
III; h(x) ≤ g(x) ≤ f (x) se, e somente se, -2 ≤ x ≤ -1
IV. g(x) ≤ f(x) ≤ h(x) se, e somente se, -2 ≤ x ≤ 0
V. g(x) ≤ h(x) ≤ f(x) se, e somente se, -2 ≤ x ≤ -1
Assinale a alternativa que contém o número de sentença(s) verdadeira(s).
Os gráficos das funçõesf (x) = 1 -x, g(x) = 6x e h(x) = -x2 + 2x + 5 estão ilustrados na Figura 1.

Analise as sentenças abaixo, em relação às informações anteriores.
I. f(x) ≤ h(x) ≤ g(x) se, e somente se, 1 ≤ x ≤ 4
II. f(x) ≤ h(x) ≤ g(x) se, e somente se, 0 ≤ x ≤ 4
III; h(x) ≤ g(x) ≤ f (x) se, e somente se, -2 ≤ x ≤ -1
IV. g(x) ≤ f(x) ≤ h(x) se, e somente se, -2 ≤ x ≤ 0
V. g(x) ≤ h(x) ≤ f(x) se, e somente se, -2 ≤ x ≤ -1
Assinale a alternativa que contém o número de sentença(s) verdadeira(s).
O valor de
x . y com x,y 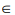 Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
O valor de
x . y com x,y 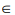 Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:


A função quadrática cujo gráfico contém os pontos (0,-9), (1,0) e (2,15) tem vértice em:


Sejam f , g e h as funções cujos gráficos estão ilustrados na Figura 3.

O intervalo que representa o conjunto ( Im ( f )∩ Im (g) ) - ( D (f)∩Im ( h) ) é :

O intervalo que representa o conjunto ( Im ( f )∩ Im (g) ) - ( D (f)∩Im ( h) ) é :
Sejam g(x) = cos x e f a função cujo gráfico está representado na Figura 1.

O produto dos valores de x que satisfazem a equação ( f ° g )( x ) = 0 , para x € ] 0,2π ] é :

O produto dos valores de x que satisfazem a equação ( f ° g )( x ) = 0 , para x € ] 0,2π ] é :