abeafa9c-fc
PUC - RJ 2018 - Matemática - Funções, Função de 2º Grau
Sejam f,g: R → R funções dadas por f(x) = 4 - x2
e
g(x) = x + b (onde b é uma constante real).
Existe um único número real x tal que f(x) = g(x)
Quanto vale b?
Sejam f,g: R → R funções dadas por f(x) = 4 - x2
e
g(x) = x + b (onde b é uma constante real).
Existe um único número real x tal que f(x) = g(x)
Quanto vale b?
A
12
B
13/2
C
15/2
D
17/4
E
18
 ?
?










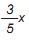
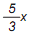





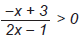 onde x
pertence ao conjunto dos números naturais é:
onde x
pertence ao conjunto dos números naturais é:



