cb8565cf-02
MACKENZIE 2019 - Matemática - Funções, Equação Logarítmica
A equação 2 log x = log 1000 + colog 10 existe para x igual a
A equação 2 log x = log 1000 + colog 10 existe para x igual a
A
1000
B
100
C
10
D
– 10
E
0






A função f (x)=  tem como domínio o conjunto solução
tem como domínio o conjunto solução





A função quadrática f, de R em R, representada graficamente, com raízes reais x1 e x2, tais que log 1,25 0,64 = x1 e log 5/3 0,6 = x2 é definida por

Se a função f : R − {2} → R* é definida por 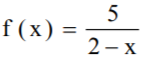 e f−1 a sua
inversa, então f -1 (-2) é igual a
e f−1 a sua
inversa, então f -1 (-2) é igual a
 e
e  . Então, podemos afirmar que
. Então, podemos afirmar queO conjunto dos números reais, para os quais a função 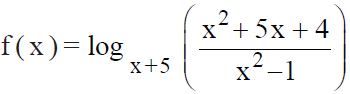 está definida, é
está definida, é
Na igualdade  , supondo x o maior valor inteiro possível, então, nesse caso, x2y vale
, supondo x o maior valor inteiro possível, então, nesse caso, x2y vale