Questõesde FUVEST sobre Funções
Sejam Df e Dg os maiores subconjuntos de R nos quais estão definidas, respectivamente, as funções reais

Considere, ainda, If e Ig as imagens de f e de g, respectivamente.
Nessas condições,
Sejam Df e Dg os maiores subconjuntos de R nos quais estão definidas, respectivamente, as funções reais

Considere, ainda, If e Ig as imagens de f e de g, respectivamente.
Nessas condições,
tanto Df e Dg quanto If e Ig diferem em mais de um ponto.
Sejam f: R→ R e g: R+→ R definidas por
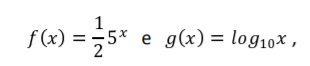
respectivamente.
O gráfico da função composta g°f é:
Sejam f: R→ R e g: R+→ R definidas por
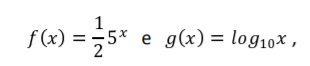
respectivamente.
O gráfico da função composta g°f é:





Se log2 y = -1/2 + 2/3 log2 x , para x > 0, então
y =
y =
y =
y =
y =
Se a função ݂: f :ℝ - { 2 } → ℝ é definida por ݂f (x) = 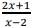 e a
função ݃ g :ℝ - { 2 } → ℝ é definida por ݃g (x) = f ( f(x) ), então
݃g(x) é igual a
e a
função ݃ g :ℝ - { 2 } → ℝ é definida por ݃g (x) = f ( f(x) ), então
݃g(x) é igual a
Se a função ݂: f :ℝ - { 2 } → ℝ é definida por ݂f (x) = 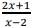 e a
função ݃ g :ℝ - { 2 } → ℝ é definida por ݃g (x) = f ( f(x) ), então
݃g(x) é igual a
e a
função ݃ g :ℝ - { 2 } → ℝ é definida por ݃g (x) = f ( f(x) ), então
݃g(x) é igual a
Uma quantidade fixa de um gás ideal é mantida a
temperatura constante, e seu volume varia com o tempo de
acordo com a seguinte fórmula:
V(t) = log2(5 + 2sen(πt)), 0 ≤ t ≤ 2,
em que t é medido em horas e V(t) é medido em m3
. A
pressão máxima do gás no intervalo de tempo [0,2] ocorre
no instante
Uma quantidade fixa de um gás ideal é mantida a temperatura constante, e seu volume varia com o tempo de acordo com a seguinte fórmula:
V(t) = log2(5 + 2sen(πt)), 0 ≤ t ≤ 2,
em que t é medido em horas e V(t) é medido em m3 . A pressão máxima do gás no intervalo de tempo [0,2] ocorre no instante
Considere as funções ƒ(x) = x2 + 4 e g(x) = 1 + log½ x,
em que o domínio de ƒ é o conjunto dos números reais e o
domínio de g é o conjunto dos números reais maiores do
que 0. Seja
h(x) = 3ƒ(g(x)) + 2g(ƒ(x)),
em que x > 0. Então, h(2) é igual a
Considere as funções ƒ(x) = x2 + 4 e g(x) = 1 + log½ x, em que o domínio de ƒ é o conjunto dos números reais e o domínio de g é o conjunto dos números reais maiores do que 0. Seja
h(x) = 3ƒ(g(x)) + 2g(ƒ(x)),
em que x > 0. Então, h(2) é igual a