6087be8d-1b
FGV 2015 - Matemática - Funções, Função de 2º Grau
O comprimento do segmento determinado pelos pontos
de intersecção das parábolas de equações y = x2 - 8x + 3 e y = -4x2 + 2x + 3 é:
O comprimento do segmento determinado pelos pontos
de intersecção das parábolas de equações y = x2 - 8x + 3 e y = -4x2 + 2x + 3 é:
A
2√37
B
3√41
C

D

E
4√45

 , sendo V o vértice da parábola.
, sendo V o vértice da parábola.
 é igual a
é igual a é
{x ∈ IR / m ≤ x ≤ n}. Em tal condição, a média aritmética
simples entre o menor valor possível para m e o maior valor
possível para n é igual a
é
{x ∈ IR / m ≤ x ≤ n}. Em tal condição, a média aritmética
simples entre o menor valor possível para m e o maior valor
possível para n é igual a






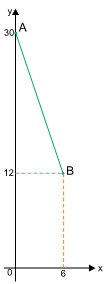
 , descrito na figura, representam o comprimento (x) e a largura (y) de um retângulo, ambos em centímetros. Por exemplo, o ponto de coordenadas (4, 18) representa um retângulo de comprimento 4 cm e largura 18 cm.
, descrito na figura, representam o comprimento (x) e a largura (y) de um retângulo, ambos em centímetros. Por exemplo, o ponto de coordenadas (4, 18) representa um retângulo de comprimento 4 cm e largura 18 cm.