Questõesde FGV sobre Funções

InícioTodas as questões
1
1
1
Foram encontradas 68 questões
1d641b1e-b0
FGV 2015 - Matemática - Funções, Equação Logarítmica

A soma dos montantes de n depósitos anuais, de valor R cada um, feitos nos anos 1, 2, 3 ...n a juros compostos e à taxa de juros anual i, calculados na data n, é dada pela fórmula: S = R


Se forem feitos depósitos anuais de R$20 000,00 à taxa anual de 20%, o número n de depósitos para que a soma dos montantes seja R$148 832,00 é:

A

B

C

D

E

1d4ac296-b0
FGV 2015 - Matemática - Funções, Função de 2º Grau

O comprimento do segmento determinado pelos pontos de intersecção das parábolas de equações

y = x2 - 8x + 3  e  y = -4x2 + 2x + 3 é:

A
2√37
B
3√41
C
7/2 √43
D
5/2 √39
E
4√45
1d280d85-b0
FGV 2015 - Matemática - Funções, Função de 2º Grau

Dada a função f(x) = x2 + 3, qual o valor da expressão

A
2x
B
2x + 1
C
2x - h
D
2x - 1
E
2x + h
804c7051-b0
FGV 2015 - Matemática - Função Logarítmica, Funções

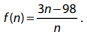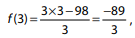Considere a função f, cujo domínio é o conjunto dos números inteiros não nulos, definida por Para alguns valores inteiros de n, o valor correspondente f ( n ) também é um número inteiro e, para outros, não. Por exemplo, para n = - 1, tem-se mas, para n = 3 , tem-se que não é um número inteiro. O número de valores inteiros de n para os quais o valor de f ( n ) também é um número inteiro é

A
14.
B
12.
C
13.
D
10.
E
11.
29b9493a-1c
FGV 2016 - Matemática - Funções, Equação Logarítmica

Estima-se que, daqui a t semanas, o número de pessoas de uma cidade que ficam conhecendo um novo produto seja dado por

Daqui a quantas semanas o número de pessoas que ficam conhecendo o produto quintuplica em relação ao número dos que o conhecem hoje?

A


B


C


D


E


8f66be72-1d
FGV 2016, FGV 2016 - Matemática - Funções, Função de 1º Grau

A única solução da equação sen 2x · sen 3x = cos 2x · cos 3x, com 0° ≤ x < 90°, é

A
72°.
B
36°.
C
24°
D
18°.
E
15°.
8f6044b0-1d
FGV 2016, FGV 2016 - Matemática - Funções, Função de 1º Grau

Na representação gráfica do sistema de equações no plano cartesiano, uma das soluções é (0, – 2). A distância entre os pontos que representam as duas outras soluções desse sistema é igual a

A
√14.
B
7/2.
C
√15/2.
D
√14/2.
E
3/2.
8f53f819-1d
FGV 2016, FGV 2016 - Matemática - Funções, Função de 1º Grau

Uma parábola P1 de equação y = x² + bx + c, quando refletida em relação ao eixo x, gera a parábola P2 . Transladando horizontalmente P1 e P2 em sentidos opostos, por quatro unidades, obtemos parábolas de equações y = f(x) e y = g(x). Nas condições descritas, o gráfico de y = (f + g)(x) necessariamente será

A
uma reta.
B
uma parábola.
C
uma hipérbole.
D
uma exponencial.
E
um círculo.
8f514f4f-1d
FGV 2016, FGV 2016 - Matemática - Funções, Equação Logarítmica

Para todos os inteiros n de 1 a 2016, temos que:



Sendo assim, a soma a1 + a2 + a3 + … + a2015 + a2016 é igual a

A
8.
B
7.
C
6.
D
-6.
E
-8.
8f4851a4-1d
FGV 2016, FGV 2016 - Matemática - Funções, Função de 1º Grau

A equação algébrica x³ – 7x² + kx + 216 = 0, em que k é um número real, possui três raízes reais. Sabendo-se que o quadrado de uma das raízes dessa equação é igual ao produto das outras duas, então o valor de k é igual a

A
– 64.
B
– 42.
C
– 36.
D
18.
E
24.
8f39cb9a-1d
FGV 2016, FGV 2016 - Matemática - Funções, Função de 1º Grau

O índice de Angstrom (IA), usado para alertas de risco de incêndio, é uma função da umidade relativa do ar (U), em porcentagem, e da temperatura do ar (T), em ºC. O índice é calculado pela fórmula , e sua interpretação feita por meio da tabela a seguir.


A temperatura T, em ºC, ao longo das 24 horas de um dia, variou de acordo com a função T(x) = – 0,2x² + 4,8x, sendo x a hora do dia (0 ≤ x ≤ 24). No horário da temperatura máxima desse dia, a umidade relativa do ar era de 35% (U = 35). De acordo com a interpretação do índice de Angstrom, nesse horário, a condição de ocorrência de incêndio era

A
improvável.
B
desfavorável.
C
favorável.
D
provável.
E
muito provável.
6199fe24-16
FGV 2018 - Matemática - Funções, Equações Exponenciais

Em determinado estado, a quantidade máxima de álcool no sangue, permitida para dirigir, é 0,06 miligrama por ml de sangue. Logo após ingerir um copo cheio de certa bebida alcoólica, a quantidade de álcool no sangue de uma pessoa sobe para 0,3 miligrama por ml de sangue.

Suponha que a quantidade de álcool no sangue desta pessoa decresça exponencialmente com o tempo de forma que, a cada hora, a quantidade de álcool por ml se reduza à metade, isto é, Q (x)=0,3 . (0 , 5)x , em que x é a variável tempo medido em horas a partir de zero (momento da ingestão da bebida) e Q(x) é a quantidade de álcool no sangue no momento x.

Depois de quanto tempo, após o consumo da bebida, a pessoa poderá voltar a dirigir?

Adote para log 2 o valor 0,3.

A
125 minutos.
B
130 minutos.
C
140 minutos.
D
120 minutos.
E
135 minutos.
61969b49-16
FGV 2018 - Matemática - Funções, Logaritmos

Quantas vezes, no mínimo, deve-se lançar um dado honesto para que a probabilidade de “sair um 5” pelo menos uma vez seja maior que 0,9?

Adote para log 2 o valor 0,3 e para log 3 o valor 0,48.

A
11
B
14
C
10
D
13
E
12
61905bf1-16
FGV 2018 - Matemática - Funções

Quantos números inteiros não negativos satisfazem a inequação x3 + 4x2 +x -6 ≤ 0?

A
2
B
Infinitos.
C
5
D
3
E
4
61899bc9-16
FGV 2018 - Matemática - Funções, Função de 1º Grau

Uma rede de livrarias estima vender anualmente 1 500 unidades de determinado livro se o seu preço unitário de venda for R$50,00. Além disso, a rede estima que uma queda de R$10,00 no preço de cada exemplar proporcionará um aumento de vendas de 100 unidades por ano.

Supondo que a relação entre preço e quantidade vendida anualmente possa ser expressa por uma função polinomial de 1º grau, quanto deverá ser cobrado por livro para maximizar a receita anual?

A
R$90,00
B
R$100,00
C
R$70,00
D
R$110,00
E
R$80,00