Questõesde FGV sobre Funções
No conjunto dos números reais, a equação exponencial 2x+2 + 8x = 4x+1 possui
Dadas as funções f(x) = x2 + 1 e g(x) = |x| + 1, ambas definidas para todos os números reais, o
gráfico da função composta f(g(x)), em linha cheia, será





De acordo com o teorema fundamental da álgebra, quando resolvida em  , a equação
algébrica x4 – 3x3 + 2x2 – 6x = 0 possui quatro raízes. A respeito dessas raízes, pode-se afirmar
que
, a equação
algébrica x4 – 3x3 + 2x2 – 6x = 0 possui quatro raízes. A respeito dessas raízes, pode-se afirmar
que
 , a equação
algébrica x4 – 3x3 + 2x2 – 6x = 0 possui quatro raízes. A respeito dessas raízes, pode-se afirmar
que
, a equação
algébrica x4 – 3x3 + 2x2 – 6x = 0 possui quatro raízes. A respeito dessas raízes, pode-se afirmar
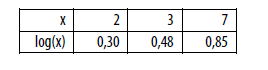
queDadas as funções (fx ) =22x e (gx) =5x , para que valor de x ocorre
a relação f[g(x)]=g[f(x)]?
Use, se necessário, a tabela abaixo:

Uma função do 1º grau f (x) possui as seguintes características:
• f(k) =− 2
• f(5) =2k +1
• O gráfico de f é uma reta com coeficiente angular igual a −3.
O valor de k é:
Uma função do 1º grau f (x) possui as seguintes características:
• f(k) =− 2
• f(5) =2k +1
• O gráfico de f é uma reta com coeficiente angular igual a −3.
O valor de k é:
O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se
ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.
Sobre os valores de a,b e c , tem-se:
O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.
Sobre os valores de a,b e c , tem-se:
A reta reta x = k intersecta os gráficos das funções y = log4 x e y = log4( x+3) nos pontos P e Q, respectivamente. A distância entre os pontos P e Q é 1/2 •
O valor de k é
A reta reta x = k intersecta os gráficos das funções y = log4 x e y = log4( x+3) nos pontos P e Q, respectivamente. A distância entre os pontos P e Q é 1/2 •
O valor de k é
Considere a seguinte tabela, em que ln( )x representa o logaritmo neperiano de x :

O valor de x que satisfaz a equação 6x =10 x
é aproximadamente igual a
Considere a seguinte tabela, em que ln( )x representa o logaritmo neperiano de x :

O valor de x que satisfaz a equação 6x =10 x
é aproximadamente igual a
A reta x=k intersecta os gráficos das funções y = log4 x e y = log4(x+3) nos pontos P e Q,
respectivamente. A distância entre os pontos P e Q é
1/2.
O valor de k é
A reta x=k intersecta os gráficos das funções y = log4 x e y = log4(x+3) nos pontos P e Q, respectivamente. A distância entre os pontos P e Q é 1/2.
O valor de k é
O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se
ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.
Sobre os valores de a,b e c , tem-se:
O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.
Sobre os valores de a,b e c , tem-se:
Considere a seguinte tabela, em que ln(x) representa o logaritmo neperiano de x :
x 1 2 3 4 5
In(x) 0 0,69 1,10 1,39 1,61
O valor de x que satisfaz a equação 6x=10 é aproximadamente igual a
Considere a seguinte tabela, em que ln(x) representa o logaritmo neperiano de x :
x 1 2 3 4 5
In(x) 0 0,69 1,10 1,39 1,61
O valor de x que satisfaz a equação 6x=10 é aproximadamente igual a
Um restaurante francês oferece um prato sofisticado ao preço de p reais por unidade. A quantidade
mensal x de pratos que é vendida relaciona-se com o preço cobrado através da função
p = -0,4x + 200 .
Sejam k1 e k2 os números de pratos vendidos mensalmente, para os quais a receita é igual a
R$ 21 000,00. O valor de K1 +k2 é:
Um restaurante francês oferece um prato sofisticado ao preço de p reais por unidade. A quantidade mensal x de pratos que é vendida relaciona-se com o preço cobrado através da função p = -0,4x + 200 . Sejam k1 e k2 os números de pratos vendidos mensalmente, para os quais a receita é igual a R$ 21 000,00. O valor de K1 +k2 é:
Para que valor de a , o conjunto imagem da função quadrática f(x) = ax2 -4x + 6 é o intervalo
[−6, ∞[ ?
O valor de mercado de um carro modelo A, daqui a t semestres é V1 = 50 000e-0,08t e o valor de
mercado de outro carro modelo B, daqui a t semestres é V2 = 50 000e-0,10t .
Após quantos semestres, contados a partir de hoje, os valores se igualarão?
Use para resolver a seguinte tabela:
x 1 2 3 4 5
ln(x) 0 0,69 1,10 1,39 1,61
Um restaurante francês oferece um prato sofisticado ao preço de p reais por unidade. A quantidade
mensal x de pratos que é vendida relaciona-se com o preço cobrado através da função
p = - 0,4x + 200. Sejam k1 e k2 os números de pratos vendidos mensalmente, para os quais a receita é igual a
R$ 21 000,00. O valor de k1 + k2 é:
Considere a aproximação: log2 = 0,3 . É correto afirmar que a soma das raízes da equação 22x - 6.2x + 5 =0 é
No plano cartesiano, há dois pontos R e S pertencentes à parábola de equação y=x2 e que estão
alinhados com os pontos A(0,3) e B(4,0).
A soma das abscissas dos pontos R e S é:
A soma dos montantes de n depósitos anuais, de valor R
cada um, feitos nos anos 1, 2, 3 ...n a juros compostos e
à taxa de juros anual i, calculados na data n, é dada pela
fórmula: S = R 
Se forem feitos depósitos anuais de R$20 000,00 à taxa
anual de 20%, o número n de depósitos para que a soma
dos montantes seja R$148 832,00 é:
A soma dos montantes de n depósitos anuais, de valor R
cada um, feitos nos anos 1, 2, 3 ...n a juros compostos e
à taxa de juros anual i, calculados na data n, é dada pela
fórmula: S = R 
Se forem feitos depósitos anuais de R$20 000,00 à taxa
anual de 20%, o número n de depósitos para que a soma
dos montantes seja R$148 832,00 é:




