Analise as afirmações:
I. Considerando x+y= 1 e x2 + y2=2, o valor de x3 + y3 é 5/2
II. Se 2 (22x) = 4x + 64 o valor de x3 = 27
III. No lançamento de dois dados, o percentual do produto dos números obtidos nos dois dados ser divisível por 2 e 3 simultaneamente é de aproximadamente 41,7%.
IV. Suponha que os gráficos de f(x)= x2 e g(x)=2x sejam feitos sobre uma malha coordenada quadriculada onde a unidade de comprimento seja 1cm. A distância de 0,12m à direita da origem, a altura do gráfico de f é um pouco maior do que 1 m e a altura do gráfico de g é maior do que a altura de um prédio de 15 andares ao considerar um pé-direito de 2,5 m ( altura padrão entre o piso e o teto.Está correto o que se afirma em:
Analise as afirmações:
Está correto o que se afirma em:

 então é correto afirmar:
então é correto afirmar:




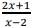 e a
função ݃
e a
função ݃

 para o universo [0,2
para o universo [0,2
 é o
conjunto dos números reais.
é o
conjunto dos números reais. 