Questõessobre Funções
O gráfico que representa mais adequadamente a função f(x) = log x é




Considere as seguintes funções exponenciais:
I. y = 0,003 x 1,2x .
II. y = 62 x(2/3)x .
III. y = 10 x 0,99x .
IV. y = 33x .
Entre essas, as funções exponenciais crescentes são:
Considere as seguintes funções exponenciais:
I. y = 0,003 x 1,2x .
II. y = 62 x(2/3)x .
III. y = 10 x 0,99x .
IV. y = 33x .
Entre essas, as funções exponenciais crescentes são:
Classifique cada uma das funções exponenciais como crescente (C) ou
decrescente (D):
I. ƒ(x) = (7/3)x .
II. g(x) = 0,2x .
III. h(x) = (1/3)x .
IV. p(x) = (5)x .
A seqüência correta dessa classificação é
Classifique cada uma das funções exponenciais como crescente (C) ou decrescente (D):
I. ƒ(x) = (7/3)x .
II. g(x) = 0,2x .
III. h(x) = (1/3)x .
IV. p(x) = (5)x .
A seqüência correta dessa classificação é
O valor da expressão 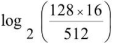 é
é
O valor da expressão 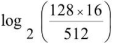 é
é
As afirmações sobre as propriedades operatórias da função logarítimica
podem ser verdadeiras (V) ou falsas (F). Verifique
I. log 10 = 1.
II. log 100 = 2.
III. log 5 < 1.
As afirmações I, II e III são, respectivamente:
As afirmações sobre as propriedades operatórias da função logarítimica podem ser verdadeiras (V) ou falsas (F). Verifique
I. log 10 = 1.
II. log 100 = 2.
III. log 5 < 1.
As afirmações I, II e III são, respectivamente:
Uma prestadora de serviços cobra pela visita à residência do cliente e pelo tempo necessário
para realizar o serviço na residência.
O valor da visita é R$ 40,00 e o valor da hora para realização do serviço é R$ 20,00.
Uma expressão que indica o valor a ser pago (P) em função das horas (h) necessárias à execução
do serviço é
Uma prestadora de serviços cobra pela visita à residência do cliente e pelo tempo necessário para realizar o serviço na residência.
O valor da visita é R$ 40,00 e o valor da hora para realização do serviço é R$ 20,00.
Uma expressão que indica o valor a ser pago (P) em função das horas (h) necessárias à execução do serviço é
O gráfico que pode representar a função dada por y = log3 x é
O gráfico que pode representar a função dada por y = log3 x é




Júlia ficou sabendo, em sua aula de Ciências, que:
I. A concentração de antibiótico na corrente sangüínea de um animal decai
exponencialmente e é dada por uma função da forma C(t) = C0at , em que C0 é a concentração de antibiótico no sangue do animal no instante em que é aplicado.
II. Uma colônia de bactérias cresce exponencialmente no corpo de um animal que não é
submetido a um tratamento, e o número de bactérias em função do tempo t é dado pela
função B(t) = B0bi , em que B0 é a quantidade inicial de bactérias no corpo do animal.
Com relação a essas duas situações, os valores de a e b são, necessariamente,
Júlia ficou sabendo, em sua aula de Ciências, que:
I. A concentração de antibiótico na corrente sangüínea de um animal decai exponencialmente e é dada por uma função da forma C(t) = C0at , em que C0 é a concentração de antibiótico no sangue do animal no instante em que é aplicado.
II. Uma colônia de bactérias cresce exponencialmente no corpo de um animal que não é submetido a um tratamento, e o número de bactérias em função do tempo t é dado pela função B(t) = B0bi , em que B0 é a quantidade inicial de bactérias no corpo do animal.
Com relação a essas duas situações, os valores de a e b são, necessariamente,
Neste ano de 2019, uma aluna de um Instituto Federal
do Rio de Janeiro, conseguiu desenvolver com seu
professor, um teorema que envolve funções do 2º grau,
denominado Teorema da Etiene, em homenagem ao seu
nome. Na prática, o teorema diz que numa função do
segundo grau y = ax² + bx + c , o ponto simétrico ao ponto
(0, c) em relação ao eixo de simetria da parábola pode ser
simplesmente encontrado pelas coordenadas do ponto
(x′ + x′′
,c ), onde x′ e x′′ são as raízes ou zeros da função
quando existentes. Baseado nesse teorema que já foi
devidamente demonstrado, qual as coordenadas do ponto
simétrico ao ponto (0,-12) em relação ao eixo de simetria da
parábola de função y = 2x² − 2x − 12?
Assinale a alternativa correta para a função f(x) = 2
x
- 1 de domínio os reais.
O gráfico de uma função do 2º grau corresponde a uma curva muito especial em matemática chamada de
Parábola. Resolva a função f(x) = x2
– 4x + 4 e assinale a única alternativa correta.
Sejam Df e Dg os maiores subconjuntos de R nos quais estão definidas, respectivamente, as funções reais

Considere, ainda, If e Ig as imagens de f e de g, respectivamente.
Nessas condições,
Sejam Df e Dg os maiores subconjuntos de R nos quais estão definidas, respectivamente, as funções reais

Considere, ainda, If e Ig as imagens de f e de g, respectivamente.
Nessas condições,
tanto Df e Dg quanto If e Ig diferem em mais de um ponto.
Sejam f: R→ R e g: R+→ R definidas por
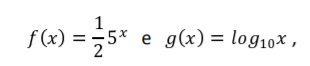
respectivamente.
O gráfico da função composta g°f é:
Sejam f: R→ R e g: R+→ R definidas por
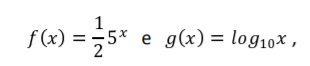
respectivamente.
O gráfico da função composta g°f é:





No plano, com o sistema de coordenadas
cartesianas usual, os gráficos das funções reais de
variável real f(x)= x2 – 6x + 9 e g(x)= –x2 + 6x – 1
são parábolas. Os pontos de interseção dessas
parábolas juntamente com seus vértices são vértices
de um quadrilátero convexo, cuja medida da área é
igual a
u. a. = unidades de área
Se x e são números reais positivos e ambos
diferentes de um, então, o valor de xu , onde  é igual a
é igual a

Se x e são números reais positivos e ambos
diferentes de um, então, o valor de xu , onde  é igual a
é igual a


A função y = Ax3 + Bx2 + Cx + D é representada pelo gráfico
a seguir. Assinale a alternativa CORRETA que fornece os
valores dos números reais A, B, C e D, respectivamente.

