Questõessobre Funções
Sejam a, b, c termos consecutivos de uma progressão
geométrica sem nenhum termo nulo e p(x) o polinômio
de grau 2 dado por p(x) = a + bx + cx2. Se a é positivo,
qual das figuras abaixo pode representar corretamente
o gráfico de p(x)?
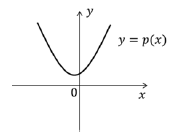
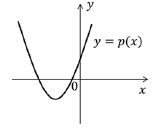
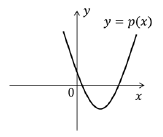
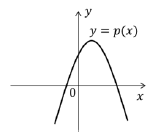
Considere o conjunto F de todas as funções
quadráticas f(x) = ax2 + 2x + 1, sendo a pertencente ao
conjunto A= {-9/2, -1, 4/9,2,13/2}. Escolhendo-se ao
acaso duas das funções de F, a probabilidade de
ambas terem raízes reais é igual a:
Um aluno traçou num mesmo plano cartesiano
os gráficos das funções afim f(x) = x + 1 e modular g(x) = |2x - 4| + x. Resolvendo a equação f(x) = g(x), determinam-se as abscissas dos pontos A(a,b) e
B(c,d), intersecção desses dois gráficos.
O valor de a + c é igual a:
Um aluno traçou num mesmo plano cartesiano os gráficos das funções afim f(x) = x + 1 e modular g(x) = |2x - 4| + x. Resolvendo a equação f(x) = g(x), determinam-se as abscissas dos pontos A(a,b) e B(c,d), intersecção desses dois gráficos.
O valor de a + c é igual a:
As retas definidas pela equações 2x + ky - 6 = 0 e -4x + (k - 1)y + 1 = 0 são paralelas.
O número real k é igual a:
As retas definidas pela equações 2x + ky - 6 = 0 e -4x + (k - 1)y + 1 = 0 são paralelas.
O número real k é igual a:
Uma pequena confecção produz exclusivamente camisas. Admita que a quantidade N de camisas produzidas
mensalmente no primeiro semestre de 2020 seja dada pela
função N(t)=125+6.2∧((t-1)), sendo t, como mostra a tabela
abaixo, o número que representa o mês do semestre.
Mês t
Janeiro 1
Fevereiro 2
Março 3
Abril 4
Maio 5
Junho 6
Com os dados acima, pode-se concluir que essa confecção produziu exatamente 173 camisas no mês de:
Considere as funções
f(x) = sen(x), g(x) = tg(x) e h(x) = 2x² + 1. É correto afirmar que é
periódica a função:
Considere a sequência 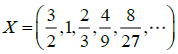 . Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
. Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
Considere a sequência 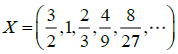 . Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
. Construindo-se uma nova sequência, cujos
termos são formados pelos logaritmos de base
2/3
dos termos da sequência
X
, tem-se que a
soma dos 30 primeiros termos desta nova sequência é:
A Figura 1 representa o gráfico da função 

A solução da inequação 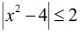 é dada por:
é dada por:
A Figura 1 representa o gráfico da função 

A solução da inequação 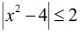 é dada por:
é dada por:





Define-se como função exponencial a relação dada por
f :
R → R tal que f (x)= ax , sendo
a∈R , a > 0
e
a ≠1.
Analise as sentenças, e assinale (V) para verdadeira e (F) para falsa.
( )f (x)=2-x não é uma função exponencial.
( ) Uma função exponencial não está definida para valores negativos de
x .
( ) f( x) = πx é uma função exponencial e intercepta o eixo das ordenadas em y =1.
( ) Toda função exponencial possui uma assíntota horizontal.
Define-se como função exponencial a relação dada por f : R → R tal que f (x)= ax , sendo a∈R , a > 0 e a ≠1. Analise as sentenças, e assinale (V) para verdadeira e (F) para falsa.
( )f (x)=2-x não é uma função exponencial.
( ) Uma função exponencial não está definida para valores negativos de x .
( ) f( x) = πx é uma função exponencial e intercepta o eixo das ordenadas em y =1.
( ) Toda função exponencial possui uma assíntota horizontal.
Qual é a variação média da função ƒ(x) = 2/(1 + e−x) no
intervalo x ∈ [0;2]?
Indique a derivada da função  com relação à
variável x, para x ≥ 0.
com relação à
variável x, para x ≥ 0.
Indique a derivada da função  com relação à
variável x, para x ≥ 0.
com relação à
variável x, para x ≥ 0.
Assinale a alternativa que expressa o resultado de 
Assinale a alternativa que expressa o resultado de 




Indique a derivada da função f(x) = 1−x2/1+x com relação à
variável x.
A figura representa o gráfico de y= ax 2 + bx + c.

Assinale a alternativa correta.
A figura representa o gráfico de y= ax 2 + bx + c.

Assinale a alternativa correta.
Sob condições ideais, o crescimento de uma cultura
de bactérias obedece à função P(t) = A ∙ e Kt , em
que P(t) é o número de bactérias no tempo t ≥ 0
horas; A e K são constantes positivas. Verifica-se
que o número inicial de bactérias, P(0), duplica a
cada 4 horas. Dessa forma, o número de bactérias
após 6 horas, em relação ao número inicial, é


Os gráficos das funções f(x) = ax 2 + bx − a e g(x) = cx + a com a, c ≠ 0 se interceptam nos
pontos (−2,0) e (1,3). As raízes da função f(x) são
A figura representa o gráfico da função f(x) = ax 2 + bx + c.

Assinale a alternativa que representa um possível
gráfico da função 
A figura representa o gráfico da função f(x) = ax 2 + bx + c.

Assinale a alternativa que representa um possível
gráfico da função 






É correto afirmar que a + b é
