Questões sobre Funções | Pratique com o Prisma

0d7407f3-c9

URCA 2019 - Matemática - Funções, Inequação Logarítmica

Se = 3 com x, y, z ∈ N e x, y, z estão em progressão geométrica nessa ordem, encontre o valor de y.

A

4

B

6

C

2

D

1

E

8

d4c81808-fc

PUC - RS 2018 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau

Considere as duas funções reais f(x) e g(x), esboçadas no plano cartesiano abaixo.

Com base no gráfico, sabendo que a = g(f(1)) - g (f(-1)), o valor de f(a + 1) é

A

1

B

0

C

-1

D

-2

b7c5570d-fc

PUC - RS 2017 - Matemática - Funções, Função de 2º Grau

A função quadrática tem diversas aplicações no nosso dia a dia. Na construção de antenas parabólicas, superfícies de faróis de carros e outras aplicações, são exploradas propriedades da parábola, nome dado à curva que é o gráfico de uma função quadrática.
Seja p(x)=mx2 +nx +1. Se p(2)=0 e p(–1)=0, então os valores de m e n são, respectivamente, iguais a

A

–1/2 e 1/2

B

– 1 e 1

C

1 e 1/2

D

–1 e –1/2

ba1ab285-fb

FGV 2012 - Matemática - Funções, Função de 2º Grau

O gráfico da função real f(x) = ax2 + bx + c é uma parábola com vértice no ponto V(-1,3). Sabe-se ainda que a equação f(x) = 0 tem duas raízes reais de sinais contrários.

Sobre os valores de a,b e c , tem-se:

A

a < 0, b > 0, c > 0

B

a < 0, b < 0, c > 0

C

a < 0, b < 0, c < 0

D

a > 0, b > 0, c < 0

E

a > 0, b > 0, c > 0

ba177521-fb

FGV 2012 - Matemática - Função Logarítmica, Funções

A reta reta x = k intersecta os gráficos das funções y = log4 x e y = log4( x+3) nos pontos P e Q, respectivamente. A distância entre os pontos P e Q é 1/2 •

O valor de k é

A

1/3

B

1/2

C

1

D

2

E

3

ef934b35-fc

PUC - PR 2017 - Matemática - Funções, Equações Exponenciais

As leis governamentais dos Estados Unidos exigem que, antes que o querosene possa ser usado como combustível de jatos, deve haver a remoção dos poluentes do querosene com uso de argila. A argila fica no interior de um tubo e cada metro do tubo remove 20% dos poluentes que entram nele. Seja P0 a quantidade inicial de poluentes e P = f(n) a quantidade de poluentes que ainda permanecem após n metros da tubulação, a função P = f(n) que melhor representa a quantidade de poluentes retidos no tubo é

A

P = P0 (1,8)n2

B

P = P0 (0,8)n

C

P = P0 (0,2)n

D

P = P0 (1,2)n

E

P = P0 (0,8)n

c196e29c-f2

Esamc 2018 - Matemática - Análise de Tabelas e Gráficos, Pontos e Retas, Geometria Analítica, Funções, Função de 1º Grau, Função de 2º Grau

Segundo o texto, quantas unidades precisam ser comercializadas para que o valor da receita se iguale ao custo de produção?

No gráfico a seguir estão representadas as funções R(x) e C(x) que indicam, respectivamente, a receita obtida na comercialização de x produtos de uma empresa e o custo de produção de tais produtos. Sabe-se que o custo fixo mensal da empresa é de R$ 2.800,00 e que cada unidade produzida gera um custo adicional de R$ 80,00.

Além disso, sabe-se que o lucro máximo na comercialização desses produtos ocorre quando a diferença entre a receita e o custo de produção é máxima (região representada no gráfico por

A

8 ou 80

B

12 ou 80

C

16 ou 75

D

10 ou 70

E

14 ou 65

c19b6af0-f2

Esamc 2018 - Matemática - Análise de Tabelas e Gráficos, Pontos e Retas, Geometria Analítica, Funções, Função de 1º Grau, Função de 2º Grau

Segundo o texto, qual é o lucro máximo que pode ser obtido pela empresa na comercialização de tais produtos?

No gráfico a seguir estão representadas as funções R(x) e C(x) que indicam, respectivamente, a receita obtida na comercialização de x produtos de uma empresa e o custo de produção de tais produtos. Sabe-se que o custo fixo mensal da empresa é de R$ 2.800,00 e que cada unidade produzida gera um custo adicional de R$ 80,00.

Além disso, sabe-se que o lucro máximo na comercialização desses produtos ocorre quando a diferença entre a receita e o custo de produção é máxima (região representada no gráfico por

A

R$ 3.600,00

B

R$ 5.800,00

C

R$ 9.600,00

D

R$ 4.200,00

E

R$ 8.400,00

4ea89b13-c2

UDESC 2018 - Matemática - Funções, Equação Logarítmica

Considerando ln 10 = 2,3, então o valor da expressão é igual a:

A

4

B

10,5

C

4α

D

2,3α²

E

1,3

4e95f2b3-c2

UDESC 2018 - Matemática - Circunferências e Círculos, Funções, Geometria Plana, Função de 2º Grau

Uma circunferência tem o seu raio variando de acordo com a imagem da função f : [2,6] —» ℜ, onde f (x) = -1/2 x2 + 3x + 4. A diferença entre o maior e o menor comprimento possível dessa circunferência é de:

A

π

B

8π

C

9π

D

8,5π

E

26π

81eee22a-f8

UEG 2017 - Matemática - Função Logarítmica, Funções

O gráfico a seguir é a representação da função

O valor de ƒ-1(-1) é

A

-1

B

0

C

-2

D

2

E

1

81d46886-f8

UEG 2017 - Matemática - Funções, Função de 2º Grau

Dadas a funções ƒ(x) = -x2 e g(x) = 2x , um dos pontos de intersecção entre as funções ƒ e g é

A

(0 , 2)

B

(2 , 4)

C

(0, - 2)

D

(- 2 , - 4)

E

(- 2 , 4)

6d56c689-f8

PUC - RJ 2019 - Matemática - Funções, Função de 2º Grau

Considere as funções f(x) = 2x2 + 3 e g(x) = x - 5.
Quais são os valores reais de x tais que g(f(x))=0?

A

0 e 1

B

0 e 2

C

1 e -1

D

2 e -2

E

√2 e -√2

f062067b-f9

IF-PR 2019 - Matemática - Funções, Função de 1º Grau

A função L(t) = 2000 x (1,5)^t representa o lucro mensal de uma empresa. O lucro dessa empresa, após 3 meses, em reais, será de:

A

9000.

B

8750.

C

7500.

D

6750.

f04f50a6-f9

IF-PR 2019 - Matemática - Funções, Função de 2º Grau

Transladando a função y1 (x) = x2 obtém-se y2 (x) = (x–2)2 . E, transladando y2 (x), resulta na função y3 (x) = (x–2)2 – 2. Em relação às funções, é correto afirmar que:

A

y1 e y2 possuem dois pontos em comum.

B

y2 e y3 possuem pontos em comum.

C

y2 (x) > y3 (x), para tudo

x ∈

.

D

y1 (x) = y3 (x), para tudo

x ∈

.

9e11a2cf-b5

IF Sudeste - MG 2016 - Matemática - Funções, Função de 2º Grau

Seja uma função real definida algebricamente pela expressão 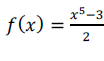. Podemos afirmar que a representação algébrica para f-1(x) será:

A

B

C

D

E

9e0578d8-b5

IF Sudeste - MG 2016 - Matemática - Funções, Equações Exponenciais

Considere a função 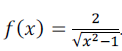. Agora marque a alternativa que possui o conjunto de maior domínio Real possível para f(x).

A

B

C

D

E

535285a2-dc

FAMEMA 2016 - Matemática - Funções, Função de 2º Grau

Em um plano cartesiano, a parábola y = –x2 + 4x + 5 e a reta y = x + 5 se intersectam nos pontos P e Q. A distância entre esses dois pontos é

A

2√3

B

√2

C

3

D

3√2

E

4

53656ff2-dc

FAMEMA 2016 - Matemática - Pontos e Retas, Geometria Analítica, Funções, Função de 2º Grau

Em um plano cartesiano, o ponto P(a, b), com a e b números reais, é o ponto de máximo da função f(x) = –x2 + 2x + 8. Se a função g(x) = 3–2x + k, com k um número real, é tal que g(a) = b, o valor de k é

A

2.

B

3.

C

4.

D

1.

E

0.

3fc24283-b5

IF-RS 2016 - Matemática - Funções, Equação Logarítmica

Considere as afirmações abaixo.

I - A equação log10x = 10x tem, pelo menos, uma solução real.
II - Para todo número real x , √x² = x .
III - A equação (x + 2) 2√x-2 = log10(1 − x) não tem soluções reais.

Assinale a alternativa que contém a(s) afirmação(ões) correta(s).

A

I

B

II

C

III

D

I e III

E

II e III

Questõessobre Funções