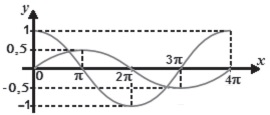
A figura indica os gráficos das funções I, II e III. Os pontos
A(72º, 0,309), B(xB, –0,309) e C(xC, 0,309) são alguns
dos pontos de intersecção dos gráficos.

Nas condições dadas, xB + xC é igual a
A figura indica os gráficos das funções I, II e III. Os pontos A(72º, 0,309), B(xB, –0,309) e C(xC, 0,309) são alguns dos pontos de intersecção dos gráficos.

Nas condições dadas, xB + xC é igual a
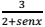 .
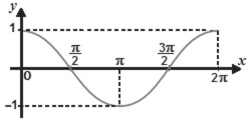
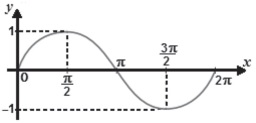
Se M e m são respectivamente os valores máximo e
mínimo que a função f assume, o valor do produto
M.m é
.
Se M e m são respectivamente os valores máximo e
mínimo que a função f assume, o valor do produto
M.m é

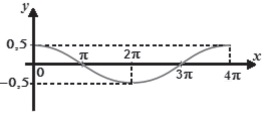
 em que
em que , pelo eixo Ox e pela reta
x = – π tem área superior a 6,5u.a..
, pelo eixo Ox e pela reta
x = – π tem área superior a 6,5u.a..