Questõessobre Funções Trigonométricas e Funções Trigonométricas Inversas
Se n é o número de soluções da equação
cos4
x - 4cos3
x + 6cos2
x – 4cosx + 1 = 0, no
intervalo [ 0, 2π ] , então o valor de n é
As funções reais f(x) = sen x e g(x) = cos x têm
seus gráficos representados no intervalo 0 ≤ x ≤ 2π.

Se a função h(x) = f(x) + g(x) tem período p e valor
máximo h, então o produto p·h é igual a

Sendo f uma função definida por f(x) = sen (x/2), 0 ≤ x ≤ 4π , então
f (x) é positiva, quando:
O valor da expressão tg 5π/3 - 3tg(210º) é:
Após simplificar a expressão numérica
tg(1)tg(89) + tg(2)tg(88) + tg(3)tg(87) +...+ tg(10)tg(80),
obtemos:
Após simplificar a expressão numérica
tg(1)tg(89) + tg(2)tg(88) + tg(3)tg(87) +...+ tg(10)tg(80),
obtemos:
O número de soluções da equação
3sen²x - 3 |senx| + cos²x = 0 que estão no
intervalo [ 0, 2 π ] é
O gráfico a seguir representa a curva de qual função trigonométrica?

O gráfico a seguir representa a curva de qual função trigonométrica?



As telhas onduladas de amianto, bastante populares, vêm tendo seu uso proibido em diversos municípios brasileiros, por ser um material cancerígeno e por também poder causar doenças respiratórias. Para substituí-las, podem ser usadas as chamadas ecotelhas — telhas onduladas produzidas a partir da reciclagem de material plástico, como, por exemplo, aparas de tubos de creme dental.
As ecotelhas têm elevada resistência mecânica, bem como à ação dos raios ultravioleta e infravermelho, além de serem econômicas, são 100% impermeáveis.
Supondo-se que a curva representativa de uma secção transversal de uma telha ondulada, como a da figura, seja definida por parte da função real f(x) = 1 − 2sen (x/2 - 5π/3) é correto afirmar que o conjunto-imagem e o período de f(x) são, respectivamente,

As telhas onduladas de amianto, bastante populares, vêm tendo seu uso proibido em diversos municípios brasileiros, por ser um material cancerígeno e por também poder causar doenças respiratórias. Para substituí-las, podem ser usadas as chamadas ecotelhas — telhas onduladas produzidas a partir da reciclagem de material plástico, como, por exemplo, aparas de tubos de creme dental.
As ecotelhas têm elevada resistência mecânica, bem como à ação dos raios ultravioleta e infravermelho, além de serem econômicas, são 100% impermeáveis.
Supondo-se que a curva representativa de uma secção transversal de uma telha ondulada, como a da figura, seja definida por parte da função real f(x) = 1 − 2sen (x/2 - 5π/3) é correto afirmar que o conjunto-imagem e o período de f(x) são, respectivamente,
Sendo A= 12 + sen2x + cos2
x, 0 < x < π/2 , é CORRETO afirmar que:
Sendo x e y as medidas de dois arcos com 0 < x < π/2 e π < y < 3π/2, respectivamente. Ao simplificar a expressão sec x/ccotg y . cossec y . sec2 y . ctg x obtém-se:
-5∫5 (ex² – (sen x)5
) dx < 0.
A função f : R → R definida por f(x) =  é contínua.
é contínua.
 é contínua.
é contínua.Ao determinar o valor da expressão (senx + cosy)2 + (seny + cosx)2
para x + y =
3π /2
, obtemos
qual dos valores indicados abaixo?
A respeito das funções trigonométricas, analise as seguintes afirmações:
I. ƒ(x) = cos (x + π) é equivalente à função g (x) = - cos (x) para todo x ∈ ℝ.
II. ƒ(x) = cos (x) é uma função par.
III. ƒ(x) = sen (x) é uma função ímpar.
IV. ƒ(x) = sen (x + π) é equivalente à função g (x) = - sen (x) para todo x ∈ ℝ.
A respeito das funções trigonométricas, analise as seguintes afirmações:
I. ƒ(x) = cos (x + π) é equivalente à função g (x) = - cos (x) para todo x ∈ ℝ.
II. ƒ(x) = cos (x) é uma função par.
III. ƒ(x) = sen (x) é uma função ímpar.
IV. ƒ(x) = sen (x + π) é equivalente à função g (x) = - sen (x) para todo x ∈ ℝ.
Nessas condições, o cosseno do ângulo  é, aproximadamente, igual a
é, aproximadamente, igual a
Nessas condições, o cosseno do ângulo  é, aproximadamente, igual a
é, aproximadamente, igual a
Leia o texto e considere as figuras para responder à questão.
Utilizando um software de desenho 3D, um tecnólogo em Mecânica elaborou o projeto de uma peça de acordo com os seguintes procedimentos:

Consideremos os seguintes números complexos:
z = 2 (cos 30º + i sen 30º) e
w = cos 120º + i sen 120º
Calculando z12 ∙ W12, devemos obter:
No plano cartesiano a seguir estão os gráficos que representam as funções f e g.

Sabendo que a curva que representa a função f é uma senóide e que o ponto destacado
(de intersecção das curvas) tem ordenada 2√2
, a lei que representa a função g é:
No plano cartesiano a seguir estão os gráficos que representam as funções f e g.

Sabendo que a curva que representa a função f é uma senóide e que o ponto destacado
(de intersecção das curvas) tem ordenada 2√2
, a lei que representa a função g é:
Um arquiteto está projetando uma escada com 16 degraus, como mostra a imagem a
seguir.

Fonte: <https://www.aarquiteta.com.br/blog/projetos-de-arquitetura/como-desenvolver-um-projeto-de-escada/>. Acesso em: 14 set 2017. (Adaptada)
Sabendo que α = 34º e que as medidas da escada da imagem estão em centímetros, a
altura x de cada degrau da escada é:
(Considere tg 34º = 0,67; sen 34º =0,56; cos 34º = 0,83)
Um arquiteto está projetando uma escada com 16 degraus, como mostra a imagem a seguir.

Fonte: <https://www.aarquiteta.com.br/blog/projetos-de-arquitetura/como-desenvolver-um-projeto-de-escada/>. Acesso em: 14 set 2017. (Adaptada)
Sabendo que α = 34º e que as medidas da escada da imagem estão em centímetros, a altura x de cada degrau da escada é:
(Considere tg 34º = 0,67; sen 34º =0,56; cos 34º = 0,83)
A expressão 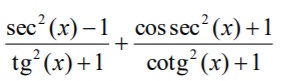 é igual a:
é igual a:
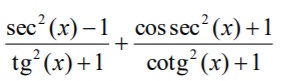 é igual a:
é igual a: