
As telhas onduladas de amianto, bastante populares, vêm tendo seu uso proibido em diversos
municípios brasileiros, por ser um material cancerígeno e por também poder causar doenças
respiratórias. Para substituí-las, podem ser usadas as chamadas ecotelhas — telhas onduladas
produzidas a partir da reciclagem de material plástico, como, por exemplo, aparas de tubos de
creme dental.
As ecotelhas têm elevada resistência mecânica, bem como à ação dos raios ultravioleta e
infravermelho, além de serem econômicas, são 100% impermeáveis.
Supondo-se que a curva representativa de uma secção transversal de uma telha ondulada, como
a da figura, seja definida por parte da função real f(x) = 1 − 2sen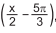 , é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,
, é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,
 , sendo t o tempo em horas
medido a partir das 6h da manhã de cada dia. Sabe-se que a temperatura ideal para a espécie criada é de 23°C. Supondo que não haja
um controle artificial da água, a temperatura ideal, em cada dia, será
atingida às:
, sendo t o tempo em horas
medido a partir das 6h da manhã de cada dia. Sabe-se que a temperatura ideal para a espécie criada é de 23°C. Supondo que não haja
um controle artificial da água, a temperatura ideal, em cada dia, será
atingida às: , sendo t o tempo em horas
medido a partir das 6h da manhã de cada dia. Sabe-se que a temperatura ideal para a espécie criada é de 23°C. Supondo que não haja
um controle artificial da água, a temperatura ideal, em cada dia, será
atingida às:
, sendo t o tempo em horas
medido a partir das 6h da manhã de cada dia. Sabe-se que a temperatura ideal para a espécie criada é de 23°C. Supondo que não haja
um controle artificial da água, a temperatura ideal, em cada dia, será
atingida às:


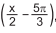 , é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente,
, é correto afirmar
que o conjunto-imagem e o período de f(x) são, respectivamente, é
é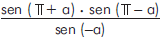 obtém-se
obtém-se