Segundo a Associação Nacional dos Fabricantes de Veículos Automotores, a produção de
automóveis teve uma queda, comparando o primeiro semestre de 2015 com o segundo semestre de
2014. Foram 3,4 milhões de unidades montadas no segundo semestre de 2014 contra 2,86 milhões
no primeiro semestre de 2015.
Disponível em: http://revistaautoesporte.globo.com. Acesso em: 8 jul. 2015 (adaptado).
A redução na produção de veículos, do segundo semestre de 2014 para o primeiro semestre de
2015, em milhão de unidade, foi de
Segundo a Associação Nacional dos Fabricantes de Veículos Automotores, a produção de automóveis teve uma queda, comparando o primeiro semestre de 2015 com o segundo semestre de 2014. Foram 3,4 milhões de unidades montadas no segundo semestre de 2014 contra 2,86 milhões no primeiro semestre de 2015.
Disponível em: http://revistaautoesporte.globo.com. Acesso em: 8 jul. 2015 (adaptado).
A redução na produção de veículos, do segundo semestre de 2014 para o primeiro semestre de 2015, em milhão de unidade, foi de

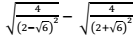 ?
?




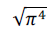 é um número racional.
é um número racional.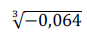 é um número racional.
é um número racional.