Questõesde FGV sobre Matemática
No plano cartesiano, uma circunferência tem centro C(5,3) e tangencia a reta de equação 3x + 4y - 12 = 0 .
A equação dessa circunferência é:
Uma senha de internet é constituída de seis letras e quatro algarismos em que a ordem é levada em
consideração. Eis uma senha possível: (a,a,b,7,7,b,a,7,a,7)
Quantas senhas diferentes podem ser formadas com quatro letras “a”, duas letras “b” e quatro
algarismos iguais a 7?
A média mínima para um aluno ser aprovado em certa disciplina de uma escola é 6.
A distribuição de frequências das médias dos alunos de uma classe, nessa disciplina, é dada abaixo:

A porcentagem de alunos aprovados foi:

Toda segunda-feira, Valéria coloca R$ 100,00 de gasolina no tanque de seu carro.
Em uma determinada segunda-feira, o preço por litro do combustível sofreu um acréscimo de 5%
em relação ao preço da segunda-feira anterior. Nessas condições, na última segunda-feira, o
volume de gasolina colocado foi x% inferior ao da segunda-feira anterior. É correto afirmar que x
pertence ao intervalo
No plano cartesiano, há dois pontos R e S pertencentes à parábola de equação y=x2 e que estão
alinhados com os pontos A(0,3) e B(4,0).
A soma das abscissas dos pontos R e S é:
Em certa região do litoral paulista, o preço do metro quadrado de terreno é R$ 400,00. O Sr.
Joaquim possui um terreno retangular com 78 metros de perímetro, sendo que a diferença entre
a medida do lado maior e a do menor é 22 metros. O valor do terreno do Sr. Joaquim é:
A soma dos montantes de n depósitos anuais, de valor R
cada um, feitos nos anos 1, 2, 3 ...n a juros compostos e
à taxa de juros anual i, calculados na data n, é dada pela
fórmula: S = R 
Se forem feitos depósitos anuais de R$20 000,00 à taxa
anual de 20%, o número n de depósitos para que a soma
dos montantes seja R$148 832,00 é:
A soma dos montantes de n depósitos anuais, de valor R
cada um, feitos nos anos 1, 2, 3 ...n a juros compostos e
à taxa de juros anual i, calculados na data n, é dada pela
fórmula: S = R 
Se forem feitos depósitos anuais de R$20 000,00 à taxa
anual de 20%, o número n de depósitos para que a soma
dos montantes seja R$148 832,00 é:





Considere o conjunto dos 51 primeiros múltiplos
positivos de 3. Seja µ sua média e M sua mediana.
Podemos afirmar que
Considere o conjunto dos 51 primeiros múltiplos positivos de 3. Seja µ sua média e M sua mediana.
Podemos afirmar que

A urna I tem duas bolas vermelhas, a urna II tem duas
bolas brancas e a urna III tem uma bola branca e outra
vermelha.
Sorteia-se uma urna e dela uma bola.
Se a bola sorteada for vermelha, qual a probabilidade de
que tenha vindo da urna I?
A urna I tem duas bolas vermelhas, a urna II tem duas bolas brancas e a urna III tem uma bola branca e outra vermelha.
Sorteia-se uma urna e dela uma bola.
Se a bola sorteada for vermelha, qual a probabilidade de
que tenha vindo da urna I?
O ponto da reta x - 3y = 5 que é mais próximo ao ponto
(1,3) tem coordenadas cuja soma é:
Os pontos de coordenadas (x-y) do plano cartesiano
que satisfazem a equação matricial  representam:
representam:
Os pontos de coordenadas (x-y) do plano cartesiano
que satisfazem a equação matricial  representam:
representam:
O comprimento do segmento determinado pelos pontos
de intersecção das parábolas de equações
y = x2 - 8x + 3 e y = -4x2 + 2x + 3 é:
Um triângulo isósceles tem a base medindo 10 e um dos
ângulos da base medindo 45°. A medida do raio da
circunferência inscrita nesse triângulo é:
A equação polinomial x3 + 12x2 - 96x - 512 = 0 tem
raízes reais em progressão geométrica quando
colocadas em ordem crescente de seus valores
absolutos. A razão dessa progressão geométrica é:
Dada a função f(x) = x2 + 3, qual o valor da expressão 
Dada a função f(x) = x2 + 3, qual o valor da expressão 
Quantos são os valores inteiros de x que satisfazem -2 < 2x + 5 < 10?
Em um posto, antes de escolher o combustível para
abastecer seu carro “flex”, um motorista verifica que o
preço do litro de gasolina é R$ 2,80. Para que seja
vantajoso, do ponto de vista exclusivamente financeiro,
abastecer seu carro com álcool, o preço máximo do litro
deste combustível deve ser


Considere a função f, cujo domínio é o conjunto dos
números inteiros não nulos, definida por 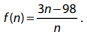 Para alguns valores inteiros de n, o valor correspondente f ( n ) também é um número inteiro e, para
outros, não. Por exemplo, para n = - 1, tem-se
Para alguns valores inteiros de n, o valor correspondente f ( n ) também é um número inteiro e, para
outros, não. Por exemplo, para n = - 1, tem-se  mas, para
n
=
3 , tem-se
mas, para
n
=
3 , tem-se 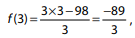 que não é um número inteiro.
O número de valores inteiros de
n para os quais o valor
de f ( n ) também é um número inteiro é
que não é um número inteiro.
O número de valores inteiros de
n para os quais o valor
de f ( n ) também é um número inteiro é
Considere a função f, cujo domínio é o conjunto dos
números inteiros não nulos, definida por 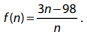 Para alguns valores inteiros de n, o valor correspondente f ( n ) também é um número inteiro e, para
outros, não. Por exemplo, para n = - 1, tem-se
Para alguns valores inteiros de n, o valor correspondente f ( n ) também é um número inteiro e, para
outros, não. Por exemplo, para n = - 1, tem-se  mas, para
n
=
3 , tem-se
mas, para
n
=
3 , tem-se 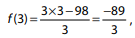 que não é um número inteiro.
O número de valores inteiros de
n para os quais o valor
de f ( n ) também é um número inteiro é
que não é um número inteiro.
O número de valores inteiros de
n para os quais o valor
de f ( n ) também é um número inteiro é
Na figura a seguir, ABCD é um quadrado de lado 6,
CN = 2 e DM =1.

A área do triângulo PMN é
Na figura a seguir, ABCD é um quadrado de lado 6, CN = 2 e DM =1.

A área do triângulo PMN é