4df63418-fd
FGV 2015 - Matemática - Trigonometria, Círculo Trigonométrico
Sabendo que x pertence ao segundo quadrante e que cos x = –0,80, pode-se afirmar que
Sabendo que x pertence ao segundo quadrante e que cos x = –0,80, pode-se afirmar que
A
cossec x = –1,666...
B
tg x = –0,75
C
sec x = –1,20
D
cotg x = 0,75
E
sen x = –0,6

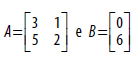 , tem
como soma de seus elementos o valor:
, tem
como soma de seus elementos o valor: 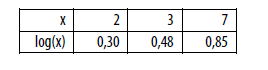
 .
. 