0fec501e-04
FGV 2020 - Matemática - Prismas, Geometria Espacial
A figura mostra um sólido composto por 30 cubos idênticos. Quando os cubos destacados em
cinza são retirados, a área total do sólido aumenta em 144 cm².

O volume do sólido original, sem a retirada dos cubos destacados em cinza, é igual a
A figura mostra um sólido composto por 30 cubos idênticos. Quando os cubos destacados em
cinza são retirados, a área total do sólido aumenta em 144 cm².

O volume do sólido original, sem a retirada dos cubos destacados em cinza, é igual a
A
1 920 cm³.
B
2 733,75 cm³.
C
3 750 cm³.
D
4 991,25 cm³
E
6 480 cm³.

 . Sabe-se que PC = PA = k e que PB = 5, em unidades de
comprimento.
. Sabe-se que PC = PA = k e que PB = 5, em unidades de
comprimento. 
 , em graus,
igual a 2α. A bissetriz do ângulo
, em graus,
igual a 2α. A bissetriz do ângulo  intersecta
intersecta  em E.
em E.
 , em cm, é igual a
, em cm, é igual a do triângulo isósceles FGV são F(6, 0) e
G(0, 6). Sendo m e n os dois valores possíveis de abscissa de V para que a área de FGV seja
igual a 6 unidades de área do plano cartesiano, o valor de m + n é
do triângulo isósceles FGV são F(6, 0) e
G(0, 6). Sendo m e n os dois valores possíveis de abscissa de V para que a área de FGV seja
igual a 6 unidades de área do plano cartesiano, o valor de m + n é


 e
e  ,
indicadas por m e n, intersectam-se no ponto C, que é centro da circunferência λ, de raio
CE = CF, como mostra a figura.
,
indicadas por m e n, intersectam-se no ponto C, que é centro da circunferência λ, de raio
CE = CF, como mostra a figura.





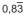
 , a equação
algébrica x
, a equação
algébrica x
 , em unidades de comprimento do plano cartesiano, é igual a
, em unidades de comprimento do plano cartesiano, é igual a
