Dada a matriz  e sabendo que a matriz
e sabendo que a matriz  é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a
equação matricial AX = B , tem como soma de seus elementos o número
é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a
equação matricial AX = B , tem como soma de seus elementos o número
Dada a matriz  e sabendo que a matriz
e sabendo que a matriz  é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a
equação matricial AX = B , tem como soma de seus elementos o número
é a matriz inversa da matriz A, podemos concluir que a matriz X, que satisfaz a
equação matricial AX = B , tem como soma de seus elementos o número
 em que x é estabelecido da
seguinte forma:
em que x é estabelecido da
seguinte forma: 
 , para todo x real não nulo.
, para todo x real não nulo. , onde
, onde 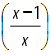 =
= 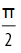 , o valor de
, o valor de