Questõesde FGV 2015 sobre Matemática

Dada a função f(x) = x2 + 3, qual o valor da expressão

Considere a função f, cujo domínio é o conjunto dos números inteiros não nulos, definida por 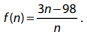Para alguns valores inteiros de n, o valor correspondente f ( n ) também é um número inteiro e, para outros, não. Por exemplo, para n = - 1, tem-se mas, para n = 3 , tem-se 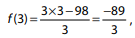que não é um número inteiro. O número de valores inteiros de n para os quais o valor de f ( n ) também é um número inteiro é

Na figura a seguir, ABCD é um quadrado de lado 6, CN = 2 e DM =1.

A área do triângulo PMN é

A soma dos montantes de n depósitos anuais, de valor R cada um, feitos nos anos 1, 2, 3 ...n a juros compostos e à taxa de juros anual i, calculados na data n, é dada pela fórmula:

Se forem feitos depósitos anuais de R$20 000,00 à taxa anual de 20%, o número n de depósitos para que a soma dos montantes seja R$148 832,00 é:

Considere o conjunto dos 51 primeiros múltiplos positivos de 3. Seja µ sua média e M sua mediana.

Podemos afirmar que

A urna I tem duas bolas vermelhas, a urna II tem duas bolas brancas e a urna III tem uma bola branca e outra vermelha.

Sorteia-se uma urna e dela uma bola.

Se a bola sorteada for vermelha, qual a probabilidade de que tenha vindo da urna I?

Ao aplicar hoje 100 mil reais a juros compostos a uma taxa de juros anual positiva, Jaime receberá 60 mil reais daqui a um ano e 55 mil reais daqui a dois anos.

Se a mesma aplicação fosse feita por dois anos a juros compostos e à mesma taxa anterior, Jaime receberia:

Os pontos de coordenadas (x,y) do plano cartesiano que satisfazem a equação matricial representam:

A quantidade mensalmente vendida x, em toneladas, de certo produto, relaciona-se com seu preço por tonelada p, em reais, através da equação p = 2000 - 0,5x.

O custo de produção mensal em reais desse produto é função da quantidade em toneladas produzidas x, mediante a relação C = 500 000 + 800 x .

O preço p que deve ser cobrado para maximizar o lucro mensal é:

Sejam 0 e 1 dois anos consecutivos. Em um país sem inflação, suponha que no ano 0 o PIB ( Produto Interno Bruto) seja 1000 e a dívida pública seja 600; portanto a relação dívida/PIB é 600/1000, ou seja 60%. Se o PIB crescer 2% ao ano e a taxa de juros da dívida pública for 4% ao ano, quanto o governo deverá economizar (isto é, ter um superávit de receitas menos despesas) no ano 1 para que a relação dívida/PIB fique estabilizada em 60%?

Nota: a dívida pública, no ano 1, cresce em relação à do ano 0 pela incorporação dos juros e diminui pelo superávit do ano 1.

Ronaldo aplicou seu patrimônio em dois fundos de investimentos, A e B.

No período de um ano ele teve um rendimento de R$ 26 250,00 aplicando 75% de seu patrimônio em A e 25% em B.

Sabendo que o fundo B rendeu uma taxa de juro anual 20% superior à de A, então, se tivesse aplicado 100% do patrimônio em A, teria recebido:

Em determinado período em que 1 dólar valia R$3,20, o custo de produção em reais de um bem exportável era assim constituído: 20% em matéria-prima e 80% em mão de obra.

Se o preço da matéria-prima subir 5% e o da mão de obra subir 10%, ambos em reais, qual deverá ser, aproximadamente, em reais, o valor de 1 dólar para que o custo de produção em dólares permaneça constante?