29a5e0e7-de
Esamc 2014 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos
Um terreno plano de forma triangular é determinado pelos pontos P, F e
R. Sabe-se que a distância entre P e F é de 120 m e que os ângulos PRF e
RPF, medem, respectivamente, 120° e 45°. Para cercar o terreno por completo, a extensão mínima da cerca deve ser um número compreendido
entre:
Um terreno plano de forma triangular é determinado pelos pontos P, F e
R. Sabe-se que a distância entre P e F é de 120 m e que os ângulos PRF e
RPF, medem, respectivamente, 120° e 45°. Para cercar o terreno por completo, a extensão mínima da cerca deve ser um número compreendido
entre:
A
240 m e 270 m
B
270 m e 300 m
C
300 m e 330 m
D
330 m e 360 m
E
360 m e 390 m








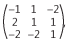 , B =
, B = 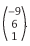 e C =
e C = 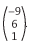 .
.
 mede
120º, AD = 2 cm e CD = 4 cm. Nessas condições, pode-se afirmar
que a área do quadrilátero ABCD é igual a:
mede
120º, AD = 2 cm e CD = 4 cm. Nessas condições, pode-se afirmar
que a área do quadrilátero ABCD é igual a:

 , traça-se o diâmetro
, traça-se o diâmetro  e duas cordas
e duas cordas  e
e  . Se é perpendicular a
. Se é perpendicular a  e o ângulo
e o ângulo  mede 30º, o ângulo mede
mede 30º, o ângulo mede  :
: