bceb793e-d9
UEM 2011 - Matemática - Funções, Equação Logarítmica
Pela fórmula do índice de expectativa de vida, nos
países afiliados à ONU, a maior expectativa de vida
não deve superar 73,2 anos.
Pela fórmula do índice de expectativa de vida, nos
países afiliados à ONU, a maior expectativa de vida
não deve superar 73,2 anos.
O principal parâmetro utilizado pela ONU para medir o
padrão de vida de um país é o Índice de Desenvolvimento
Humano (IDH). O IDH leva em conta três parâmetros:
índice de expectativa de vida, índice educacional e índice
de renda. Cada um dos três índices é calculado de modo a
fornecer um número entre 0 e 1, sendo que, quanto mais
próximo de 1, melhor o indicador. Os índices de renda e
de expectativa de vida, por exemplo, são dados,
respectivamente, pelas fórmulas  e
e  , em que x
é o produto nacional bruto per capita anual, em dólares;
ln é o logaritmo neperiano (base e); e y representa a
expectativa de vida média do país, em anos. O IDH é a
raiz cúbica do produto desses três índices. A antiga
versão do cálculo do IDH (utilizada até 2010) era obtida
pela média aritmética simples desses três índices. A partir
das informações fornecidas e de seus conhecimentos
sobre esse tema, assinale o que for correto.
, em que x
é o produto nacional bruto per capita anual, em dólares;
ln é o logaritmo neperiano (base e); e y representa a
expectativa de vida média do país, em anos. O IDH é a
raiz cúbica do produto desses três índices. A antiga
versão do cálculo do IDH (utilizada até 2010) era obtida
pela média aritmética simples desses três índices. A partir
das informações fornecidas e de seus conhecimentos
sobre esse tema, assinale o que for correto.
C
Certo
E
Errado

 .
.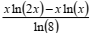 .
.