0abb4ef1-0d
UECE 2016 - Matemática - Álgebra, Trigonometria, Equação do 2º Grau e Problemas do 2º Grau, Lei dos Cossenos
Em um plano, munido do referencial cartesiano
usual, seja A o ponto de interseção das retas
3x + y + 4 = 0 e 2x – 5y + 14 = 0. Se os pontos B e
C são respectivamente as interseções de cada uma
destas retas com o eixo-x, então, a área do triângulo
ABC, é igual a

Em um plano, munido do referencial cartesiano usual, seja A o ponto de interseção das retas 3x + y + 4 = 0 e 2x – 5y + 14 = 0. Se os pontos B e C são respectivamente as interseções de cada uma destas retas com o eixo-x, então, a área do triângulo ABC, é igual a

A
13/3 u.a
B
14/3 u.a
C
16/3 u.a
D
17/3 u.a
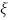 cuja parte imaginária é positiva. A parte real de
cuja parte imaginária é positiva. A parte real de 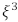 é igual a
é igual a
 , mas
em sentidos contrários. No momento em que eles se encontram,
Alfredo havia percorrido 18 km a mais do que Breno.
Logo depois do encontro, eles continuam suas caminhadas
sendo que Alfredo leva 4 horas para chegar em B, percorrendo
x quilômetros, e Breno leva 9 horas para chegar em A.
Admitindo-se que Alfredo e Breno fizeram suas caminhadas
com velocidades constantes durante todo o tempo, x será a
raiz positiva da equação
, mas
em sentidos contrários. No momento em que eles se encontram,
Alfredo havia percorrido 18 km a mais do que Breno.
Logo depois do encontro, eles continuam suas caminhadas
sendo que Alfredo leva 4 horas para chegar em B, percorrendo
x quilômetros, e Breno leva 9 horas para chegar em A.
Admitindo-se que Alfredo e Breno fizeram suas caminhadas
com velocidades constantes durante todo o tempo, x será a
raiz positiva da equação
