Questõessobre Derivada
A classificação do som como forte ou fraco
está relacionada ao nível de intensidade sonora, medida em watt/m². A menor intensidade sonora audível ou limiar de audibilidade
possui intensidade I0=10–12W/m². A relação
entre as intensidades sonoras permite calcular o nível sonoro do ambiente que é
dado em decibéis. Em virtude dos valores
das intensidades serem muito pequenos
ou muito grandes, utiliza-se as noções de
logaritmos na seguinte fórmula capaz de
calcular níveis sonoros:

onde:
NS = Nível sonoro
I = Intensidade de som considerada
I0 = Limiar de audibilidade
Disponível em:<http://mundoeducacao.bol.uol.com.br/matematica/medindo-intensidade-dos-sons>. Acessado em 08 de agosto de 2018.
Com base no texto acima, podemos afirmar que o nível sonoro em uma avenida
de tráfego intenso com intensidade de som
I=108
, em W/m², é igual a:
A classificação do som como forte ou fraco está relacionada ao nível de intensidade sonora, medida em watt/m². A menor intensidade sonora audível ou limiar de audibilidade possui intensidade I0=10–12W/m². A relação entre as intensidades sonoras permite calcular o nível sonoro do ambiente que é dado em decibéis. Em virtude dos valores das intensidades serem muito pequenos ou muito grandes, utiliza-se as noções de logaritmos na seguinte fórmula capaz de calcular níveis sonoros:

onde:
NS = Nível sonoro
I = Intensidade de som considerada
I0 = Limiar de audibilidade
Disponível em:<http://mundoeducacao.bol.uol.com.br/matematica/medindo-intensidade-dos-sons>
O Cálculo Diferencial e Integral é uma disciplina ministrada em muitos cursos de graduação. Nela são
utilizados conhecimentos matemáticos estudados ao longo do Ensino Básico.
Em uma questão de prova de Cálculo, os alunos precisavam utilizar conhecimentos de funções exponencial
e logarítmica para encontrar o ponto
(x,y)
que satisfaz simultaneamente as equações:
10.(2 - ln x) -10 = 0
e
y = 10x.(2 - ln x).
Ao desenvolver as contas, as coordenadas do ponto (x,y) que deveriam ser encontradas eram:
O excedente do consumidor dá a diferença entre o valor que o consumidor está disposto a gastar e o valor efetivamente gasto por ele na aquisição de um determinado produto. O excedente do produtor dá a diferença entre o valor real obtido pelos produtores na oferta de um produto e o valor mínimo que estão dispostos a receber pela oferta de um produto. Graficamente, os excedentes do consumidor e do produtor correspondem, respectivamente, às áreas da região pontilhada EC e da região sombreada EP, em que D(p) é a função demanda, O(p) é a função oferta e Po é o ponto de equilíbrio dessas funções. Com base nessas informações, considerando D(p) = – 6p² + 150 e O(p) = 3p² + 69, pode-se afirmar:

O excedente do produtor, EP, é igual a 285  (3p²
+ 69) dp.
(3p²
+ 69) dp.

O excedente do consumidor dá a diferença entre o valor que o
consumidor está disposto a gastar e o valor efetivamente gasto por ele
na aquisição de um determinado produto.
O excedente do produtor dá a diferença entre o valor real obtido
pelos produtores na oferta de um produto e o valor mínimo que estão
dispostos a receber pela oferta de um produto.
Graficamente, os excedentes do consumidor e do produtor
correspondem, respectivamente, às áreas da região pontilhada EC e
da região sombreada EP, em que D(p) é a função demanda, O(p) é a
função oferta e Po é o ponto de equilíbrio dessas funções.
Com base nessas informações, considerando D(p) = – 6p² + 150
e O(p) = 3p² + 69, pode-se afirmar:

A soma dos excedentes do consumidor e do produtor é dada por  (9p²
– 81) dp.
(9p²
– 81) dp.

Em uma aula de exercícios, um professor de Matemática propôs aos seus alunos a construção
do gráfico da função real definida por 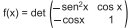 , 0 ≤ x ≤ π.
, 0 ≤ x ≤ π.
Cinco gráficos distintos, dados a seguir, foram esboçados pelos alunos.
Dentre eles, o que melhor representa a função f é
Em uma aula de exercícios, um professor de Matemática propôs aos seus alunos a construção
do gráfico da função real definida por 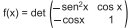 , 0 ≤ x ≤ π.
, 0 ≤ x ≤ π.
Cinco gráficos distintos, dados a seguir, foram esboçados pelos alunos.
Dentre eles, o que melhor representa a função f é





Derivada é um importante conceito trabalhado no ensino superior, especialmente nas disciplinas de
Cálculo Diferencial e Integral. A sua definição se baseia, intuitivamente, na inclinação da reta tangente ao
esboço do gráfico da função f(x) que se deseja derivar, e com um maior rigor matemático, ao limh→0 f(x+h)-f(x)/h . Em relação à função f(x) = x² (para x≥0), concluímos que os valores do domínio
que determina a imagem 4 e de f(x+h) são, respectivamente:
O Cálculo Diferencial e Integral é uma disciplina ministrada em muitos cursos de graduação. Nela são
utilizados conhecimentos matemáticos estudados ao longo do Ensino Básico.
Em uma questão de prova de Cálculo, os alunos precisavam utilizar conhecimentos de funções exponencial
e logarítmica para encontrar o ponto
(x, y)
que satisfaz simultaneamente as equações:
10.(2 - ln x) -10 = 0
e
y = 10x.(2 - ln x).
Ao desenvolver as contas, as coordenadas do ponto
(x, y)
que deveriam ser encontradas eram:
Sendo f : R2 – {(0, 0)} → R a função definida por f(x, y) = ln(x2 + 4y2), é correto afirmar:
A derivada direcional de f no ponto (2, 1), segundo o vetor  = (4/5, 3/5) é igual a 1.
= (4/5, 3/5) é igual a 1.
Sendo f : R2 – {(0, 0)} → R a função definida por f(x, y) = ln(x2 + 4y2), é correto afirmar:
A derivada direcional de f no ponto (2, 1), segundo o vetor  = (4/5, 3/5) é igual a 1.
= (4/5, 3/5) é igual a 1.
Se f : ] 0, + ∞ [ → R é uma função derivável que satisfaz a ∫ x2 f'(x)dx = x3 + c, então o gráfico de f está
contido em uma reta.
Sejam f : R → R e g : R → R funções deriváveis. Se f é invertível, f(0) = 2, g'(2) = 3 e g(f(x)) = arctg(x), para
todo x ∈ R, então (f –1)'(2) = 4.
A função f : R → R definida por f(x) = 2x + 1, se x < 1 é derivável.
x² + 1, se x > 1
A função f : R → R definida por f(x) = 2x + 1, se x < 1 é derivável.
x² + 1, se x > 1
Seja F : R3 → R a função definida por F(x, y, z) = x2 + 4y2 – z2 , é correto afirmar:
O vetor gradiente de F no ponto (1, 1, 2) é dado por  (1, 1, 2) = (2, 8, –4).
(1, 1, 2) = (2, 8, –4).
Seja F : R3 → R a função definida por F(x, y, z) = x2 + 4y2 – z2 , é correto afirmar:
O vetor gradiente de F no ponto (1, 1, 2) é dado por  (1, 1, 2) = (2, 8, –4).
(1, 1, 2) = (2, 8, –4).
Se f : R2 → R é a função definida por f(x, y) = pode-se concluir que
pode-se concluir que  (1, 1) = 7.
(1, 1) = 7.
Se f : R2 → R é a função definida por f(x, y) = pode-se concluir que
pode-se concluir que  (1, 1) = 7.
(1, 1) = 7.
Sendo f : R2 – {(0, 0)} → R a função definida por f(x, y) = ln(x2 + 4y2), é correto afirmar:
A derivada direcional de f no ponto (2, 1), segundo o vetor  = (4/5 , 3/5), é igual a 1.
= (4/5 , 3/5), é igual a 1.
Sendo f : R2 – {(0, 0)} → R a função definida por f(x, y) = ln(x2 + 4y2), é correto afirmar:
A derivada direcional de f no ponto (2, 1), segundo o vetor  = (4/5 , 3/5), é igual a 1.
= (4/5 , 3/5), é igual a 1.
Marque C, se a proposição é certo ; E, se a proposição é errado.
De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) (2x + 4) ex =. Assim, é correto afirmar:
O menor valor de f é dado por f(– 2).
De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) (2x + 4) ex =. Assim, é correto afirmar:
O menor valor de f é dado por f(– 2).
Marque C, se a proposição é certo ; E, se a proposição é errado.
De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) (2x + 4) ex =. Assim, é correto afirmar:
O gráfico de f tem concavidade voltada para cima.
De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) (2x + 4) ex =. Assim, é correto afirmar:
O gráfico de f tem concavidade voltada para cima.
Marque C, se a proposição é certo ; E, se a proposição é errado.
De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) (2x + 4) ex =. Assim, é correto afirmar:
A função f é crescente no intervalo ]−∞ −, 2[ .
De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) (2x + 4) ex =. Assim, é correto afirmar:
A função f é crescente no intervalo ]−∞ −, 2[ .
Marque C, se a proposição é certo ; E, se a proposição é errado.
De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) (2x + 4) ex =. Assim,
é correto afirmar:
A função f é contínua.
De uma função f, de domínio R, sabe-se que sua derivada f ' é definida por f '(x) (2x + 4) ex =. Assim, é correto afirmar:
A função f é contínua.