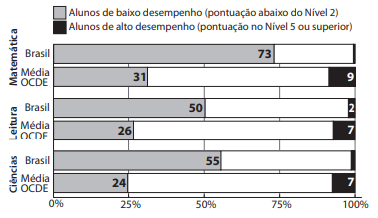
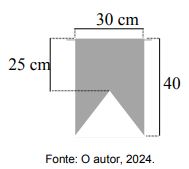
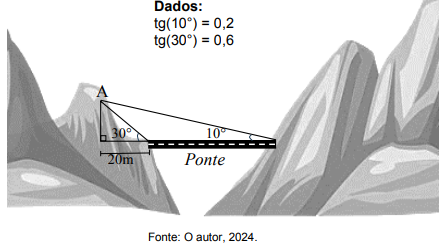
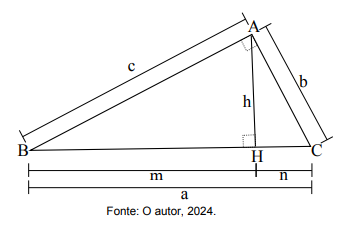
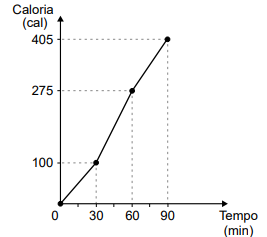
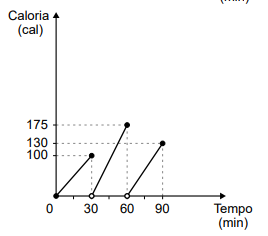
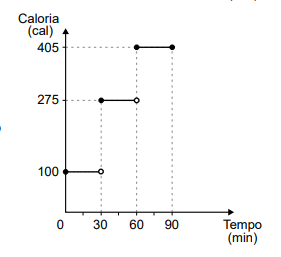
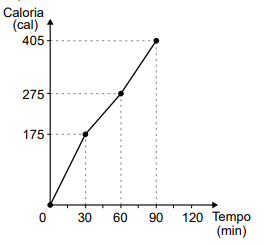
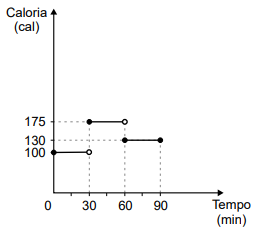
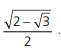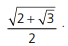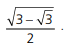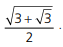A figura a seguir mostra um triângulo ABC que contém dois
quadrados em seu interior.
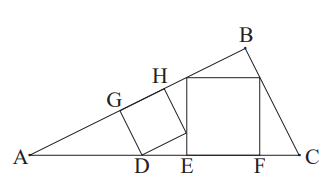
O segmento GH é lado de um dos quadrados e está contido
no segmento AB. O segmento EF, contido no segmento AC, é
lado do outro quadrado. Sabendo que AG mede 4 cm e que o
lado GH do quadrado menor mede 3 cm, o comprimento do
segmento EF é:
A figura a seguir mostra um triângulo ABC que contém dois quadrados em seu interior.

O segmento GH é lado de um dos quadrados e está contido no segmento AB. O segmento EF, contido no segmento AC, é lado do outro quadrado. Sabendo que AG mede 4 cm e que o lado GH do quadrado menor mede 3 cm, o comprimento do segmento EF é: