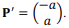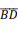Para a testagem do módulo matemático de um sistema de
IA, solicitou-se que ele gerasse, em um plano cartesiano xOy,
uma circunferência que passa pelos pontos A = (5, 0), B = (0, 3) e
C = (0, 10), e, em seguida, que descrevesse estratégias para que
fosse encontrado o centro da circunferência por meio da
utilização de régua e compasso. Como resposta, o sistema de IA
forneceu a figura e as estratégias a seguir.
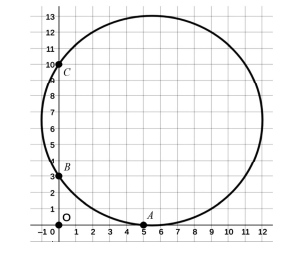
Estratégias:
• trace uma reta r que passe pelos pontos B e C;
• trace, no ponto C, uma reta s que seja perpendicular à reta r;
• denomine D o novo ponto em que a reta ; cruza a circunferência;
• ache o ponto médio do segmento 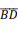 , que é o centro da circunferência, e o denomine E.
, que é o centro da circunferência, e o denomine E.

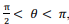
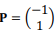
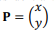
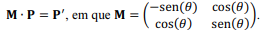
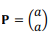 em
em