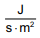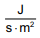b5c11bd5-4c
ENEM 2023 - Matemática - Aritmética e Problemas, Sistema de Unidade de Medidas
Em radiometria, a potência radiante emitida por
uma fonte de radiação é diretamente proporcional à
quantidade de energia, em joule (J), irradiada pela fonte,
e inversamente proporcional ao intervalo de tempo,
em segundo (s), que a fonte necessita para emitir essa
energia. Por meio de sensores adequados, localizados
em diferentes distâncias da fonte, medidas em metro (m),
é possível medir a potência radiante por unidade de área
que chega àquela posição.
A expressão que representa a unidade de medida para a
grandeza potência radiante por unidade de área é
Em radiometria, a potência radiante emitida por
uma fonte de radiação é diretamente proporcional à
quantidade de energia, em joule (J), irradiada pela fonte,
e inversamente proporcional ao intervalo de tempo,
em segundo (s), que a fonte necessita para emitir essa
energia. Por meio de sensores adequados, localizados
em diferentes distâncias da fonte, medidas em metro (m),
é possível medir a potência radiante por unidade de área
que chega àquela posição.
A expressão que representa a unidade de medida para a
grandeza potência radiante por unidade de área é
A
J ⋅ s ⋅ m2
B
J ⋅ s ⋅ m
C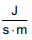
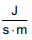
D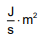
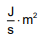
E