Uma pessoa começou a fazer caminhada em torno de uma praça circular, andando sempre
no mesmo sentido, de modo que, a cada dia, a caminhada era iniciada em um ponto diferente
da praça: P1, no primeiro dia, P2, no segundo dia, P3, no terceiro dia, e assim sucessivamente.
Sabendo-se que P1, P2, P3... são pontos da circunferência que contorna a praça, tais que cada
setor  mede 48°
, pode-se afirmar que essa pessoa iniciou a caminhada em
P1 pela segunda vez, no
mede 48°
, pode-se afirmar que essa pessoa iniciou a caminhada em
P1 pela segunda vez, no
Uma pessoa começou a fazer caminhada em torno de uma praça circular, andando sempre
no mesmo sentido, de modo que, a cada dia, a caminhada era iniciada em um ponto diferente
da praça: P1, no primeiro dia, P2, no segundo dia, P3, no terceiro dia, e assim sucessivamente.
Sabendo-se que P1, P2, P3... são pontos da circunferência que contorna a praça, tais que cada
setor  mede 48°
, pode-se afirmar que essa pessoa iniciou a caminhada em
P1 pela segunda vez, no
mede 48°
, pode-se afirmar que essa pessoa iniciou a caminhada em
P1 pela segunda vez, no




 da circunferência de equação (x – 4)
da circunferência de equação (x – 4) forma com o eixo x, então tgα é:
forma com o eixo x, então tgα é: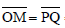 = 2cm
, e 3cm o comprimento do
arco PM, o comprimento do arco QN será:
= 2cm
, e 3cm o comprimento do
arco PM, o comprimento do arco QN será:

